A heat engine using a diatomic gas follows the cycle shown in FIGURE P21.55. Its temperature at point 1 is 20℃. a. Determine Wₛ, Q, and ∆Eₜₕ for each of the three processes in this cycle. Display your results in a table.

Key Concepts

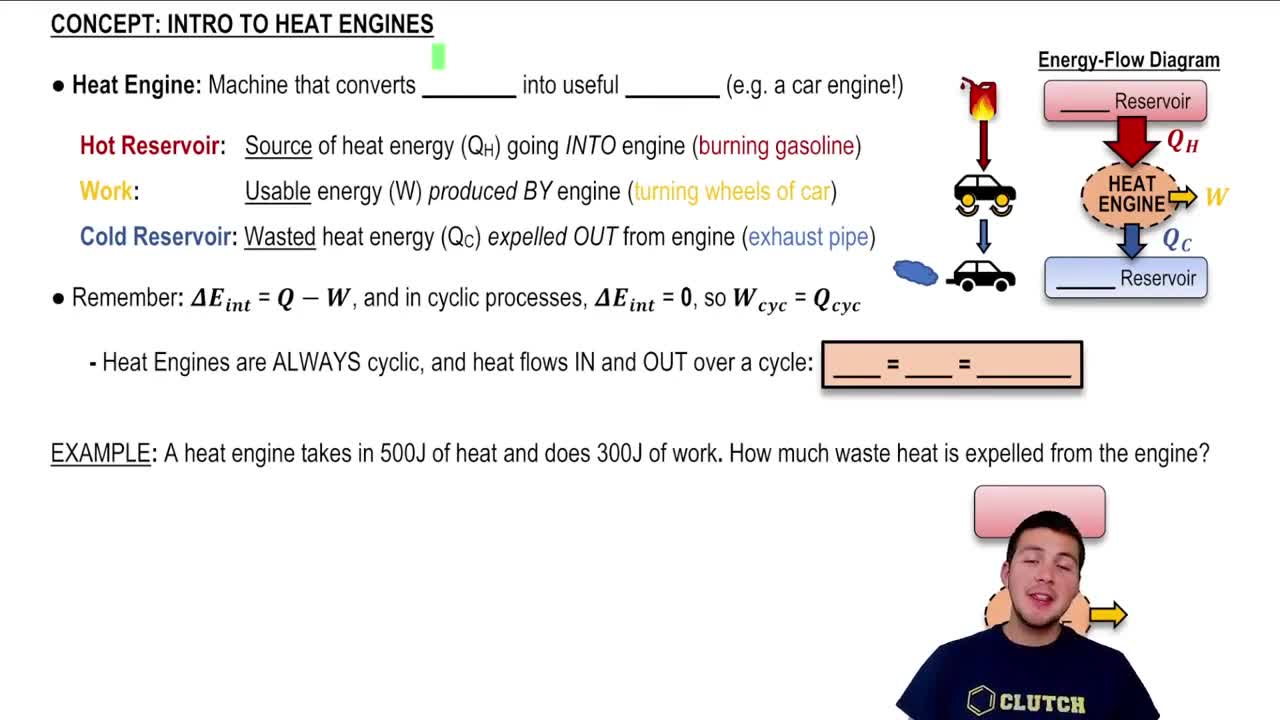
Heat Engine

A heat engine is a device that converts thermal energy into mechanical work by exploiting the temperature difference between a hot reservoir and a cold reservoir. It operates through a cyclic process, absorbing heat from the hot reservoir, performing work, and releasing some heat to the cold reservoir. The efficiency of a heat engine is determined by the ratio of work output to heat input.

First Law of Thermodynamics

The First Law of Thermodynamics states that energy cannot be created or destroyed, only transformed from one form to another. In the context of a heat engine, this law can be expressed as ΔU = Q - W, where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system. This principle is essential for analyzing energy transfers in thermodynamic processes.

Diatomic Gas Properties

Diatomic gases, such as nitrogen and oxygen, consist of molecules made up of two atoms. They exhibit specific heat capacities that differ from monatomic gases, particularly in their ability to store energy in rotational and vibrational modes. Understanding the properties of diatomic gases is crucial for calculating work done and heat transfer in thermodynamic cycles, as their behavior under varying temperatures and pressures influences the engine's performance.