Here are the essential concepts you must grasp in order to answer the question correctly.
Bernoulli's Principle
Bernoulli's Principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure. In the context of a hurricane, as the wind speed increases over the roof, the pressure above the roof decreases compared to the pressure inside the building, leading to a pressure difference that can cause structural damage.
Recommended video:
Diffraction with Huygen's Principle
Pressure Difference
Pressure difference refers to the variation in pressure between two points in a fluid. It is crucial in understanding how forces act on surfaces, such as roofs during a hurricane. The pressure difference can be calculated using Bernoulli's equation, which relates the speed of the fluid and the pressure exerted on surfaces.
Recommended video:
Pressure and Atmospheric Pressure
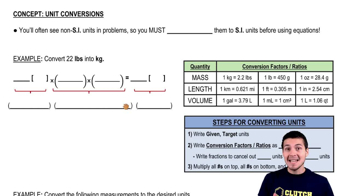
Conversion of Units
In physics, it is often necessary to convert units to ensure consistency in calculations. In this problem, the wind speed is given in kilometers per hour (km/h) and must be converted to meters per second (m/s) for use in calculations involving pressure. This conversion is essential for accurately applying formulas that involve speed and pressure.
Recommended video: