Ch 11: Impulse and Momentum
Chapter 11, Problem 11
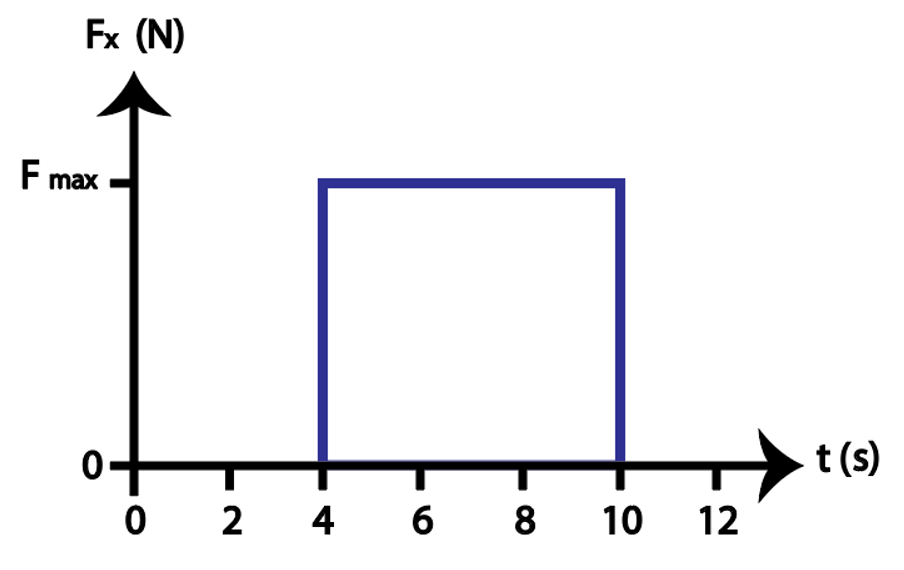
In FIGURE EX11.5, what value of Fmax gives an impulse of 6.0 N s?
 Verified Solution
Verified SolutionVideo duration:
2m633
views
Was this helpful?
Video transcript
Related Practice
Textbook Question
A white ball traveling at 2.0 m/s hits an equal-mass red ball at rest. The white ball is deflected by 25°and slowed to 1.5 m/s.
b. What percentage of the initial mechanical energy is lost in the collision?
836
views
Textbook Question
What impulse does the force shown in FIGURE EX11.3 exert on a 250 g particle?
496
views
Textbook Question
What is the impulse on a 3.0 kg particle that experiences the force shown in FIGURE EX11.4?
885
views
1
comments
Textbook Question
A 2.0 kg object is moving to the right with a speed of when it experiences the force shown in FIGURE EX11.9. What are the object's speed and direction after the force ends?
586
views
Textbook Question
Far in space, where gravity is negligible, a 425 kg rocket traveling at 75 m/s in the +x-direction fires its engines. FIGURE EX11.10 shows the thrust force as a function of time. The mass lost by the rocket during these 30 s is negligible. (b) At what time does the rocket reach its maximum speed? What is the maximum speed?
436
views
Textbook Question
A 30 g dart traveling horizontally hits and sticks in the back of a 500 g toy car, causing the car to roll forward at 1.4 m/s. What was the speed of the dart?
461
views