A 50 g ice cube can slide up and down a frictionless 30° slope. At the bottom, a spring with spring constant 25 N/m is compressed 10 cm and used to launch the ice cube up the slope. How high does it go above its starting point?

Question

Accepted Answer

Welcome back, everyone. We are making observations about the following system here. We have an incline. So let me go ahead and draw out our incline with the correct angles here. Perfect. And what we have is a experiment in which there is a spring at the bottom of the incline. Now the spring will be compressed to launch a block up and down that very incline. Now, the incline makes a 40 degree angle with the horizontal and we are called a couple of different other things about this system. You're told that the mass of the block being launched is 80 g or 800.8 kg. And we are told that the spring is compressed to millimeters or 1500.15 m. Now, the spring force constant is going to be 80 newtons per meter and we are tasked with finding what is going to be the final height of our block once it moves up the inclined surface here. So what are we going to use for this? We have springs, we have heights, we have incline. 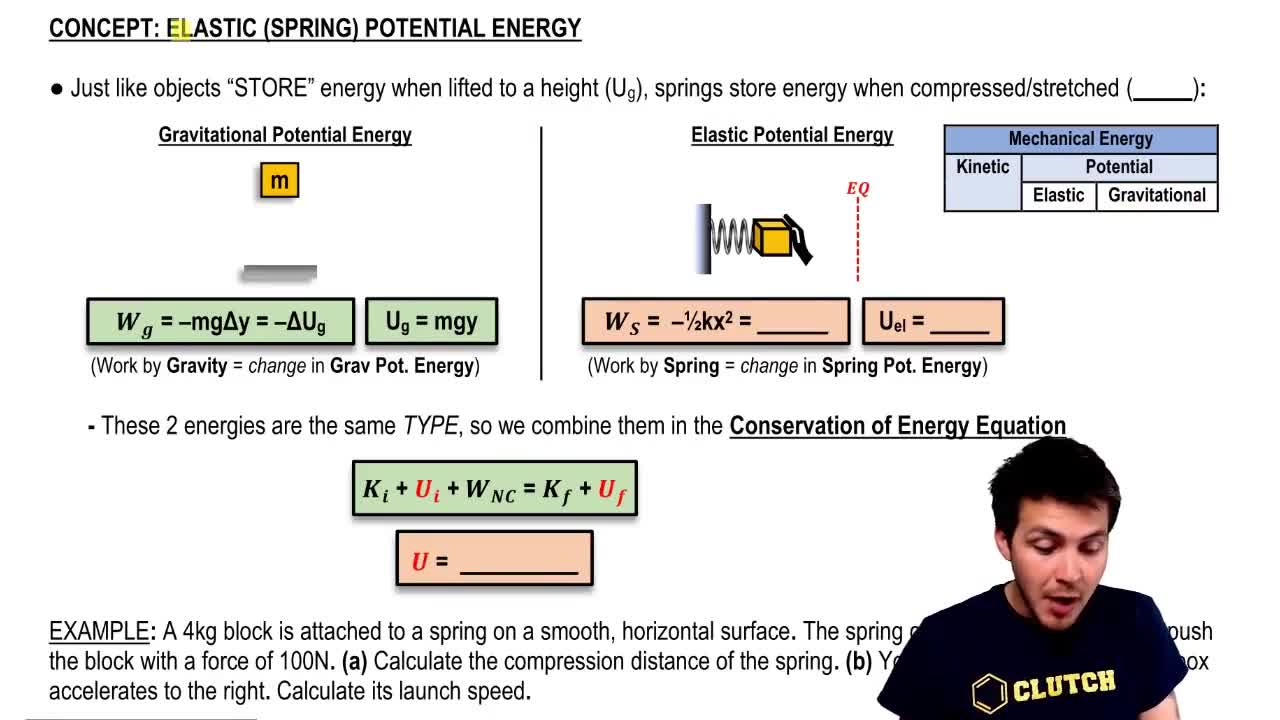What we can go ahead and use is the principle of the conservation of energy that states that our summation of our final energies is going to be equal to the summation of our initial energy. Something like this. Our final kinetic energy plus our final spring potential energy plus our final gravitational potential energy is equal to our initial kinetic energy plus our initial spring potential energy plus our initial gravitational potential energy. And we actually have formulas for each of these terms. So let's actually go ahead and expand out this equation here. What we have is we have one half times the mass of our final velocity squared plus one half times our spring constant times our final deformation squared plus uh let's see, mass times gravity times our final height times one half times our mass times our initial velocity plus one half times K times our initial deformation squared plus M G times our original height. Now, what are a couple of things we know about this system? Well, we know that it's the block starts from rest. So its initial velocity will be zero. And when it reaches its maximum point, it's going to turn around, which means at its final velocity, it'll pause for a second. So we can say that its final velocity is zero at the height that we want. Now, if we let's take the initial or the maximum deformation of the spring where the block is going to start off, we'll just say that that is a height of zero m. So we're measuring height from that point. And then we also have that our final spring deformation since the spring will no longer be compressed is also going to be zero. So, plugging in all of the terms that we know, what does this leave us with? Well, what we have is M G times our final height, which is what we desire is equal two because it's zero plus zero plus is equal to zero plus one half times our spring, constant times our initial compression squared plus zero. What I'm gonna do is I'm actually gonna move this out to the center here because we are going to manipulate this equation just a little bit. So here's what I want to do in order to isolate my final height term, I'm going to divide both sides of the equation by mass times gravity. Now, what does this give us? I'm actually going to scroll down just a little bit to give us a little bit more room. What this gives us is that our final height is equal to our spring, constant times our initial compression length squared of the spring time times two times our mass times gravity. So let's just go ahead and plug in all of those terms. We have that this is equal to 80 times 800. squared divided by two times 20.8 times 9.8, which gives us a final height of 1.15 m, which corresponds to our final answer choice of c Thank you all so much for watching. I hope this video helped. We will see you all in the next one.

A 50 g ice cube can slide up and down a frictionless 30° slope. At the bottom, a spring with spring constant 25 N/m is compressed 10 cm and used to launch the ice cube up the slope. How high does it go above its starting point?

Verified Solution

Key Concepts

Conservation of Energy

Spring Potential Energy

Gravitational Potential Energy