Large stars can explode as they finish burning their nuclear fuel, causing a supernova. The explosion blows away the outer layers of the star. According to Newton's third law, the forces that push the outer layers away have reaction forces that are inwardly directed on the core of the star. These forces compress the core and can cause the core to undergo a gravitational collapse. The gravitational forces keep pulling all the matter together tighter and tighter, crushing atoms out of existence. Under these extreme conditions, a proton and an electron can be squeezed together to form a neutron. If the collapse is halted when the neutrons all come into contact with each other, the result is an object called a neutron star, an entire star consisting of solid nuclear matter. Many neutron stars rotate about their axis with a period of ≈ 1 s and, as they do so, send out a pulse of electromagnetic waves once a second. These stars were discovered in the 1960s and are called pulsars. (e) What is the radius of a geosynchronous orbit?

Question

Accepted Answer

Hello, fellow physicists today, we're gonna solve the following practice problem together. So first off, let's read the problem and highlight all the key pieces of information that we need to use. In order to solve this problem. The explosion of large stars causes a supernova. The remnants of a supernova explosion may lead to the formation of highly magnetized and compact object called a magnetar magnetar are a type of neutron star magnetar are thought to be the source of some of the most energetic and powerful explosions in the universe such as gamma ray bursts, magnetos rotate about their access at a rate of once every 9.0 seconds. Find the radius of its geosynchronous orbit. Consider the mass of a magnetar is 2. multiplied by 10 to the power of 30 kg. OK. So our end goal is to find the radius of the geosynchronous orbit given that we're given the rotation about the axis at a rate of nine seconds. And we're also given the mass of the magnetar. Awesome. So we're given some multiple choice answers here and they're all in the same units of meters. So let's read them off to see what our final answer might be. A, is 3.80 multiplied by 10 to the power of 10. B is 1.95 multiplied by 10 to the power of 10 C is 3.80 multiplied by 10 to the power of 20 D is 7. multiplied by 10 to the power of six. OK. So first off, let us assume that a magnetar is a spherical mass. So we can recall and use the equation for an orbiting satellite. The period for an orbit of a satellite is and let's call it equation one that the period capital T. So the period squared is equal to four pi squared multiplied by radius of the orbit cubed divided by the gravitational constant multiplied by the mass of the magnetar, which we'll call it capital M subscript S the mass of the magnetar. OK. So note that our end goal is to find the radius of the geosynchronous orbit. So we need to rearrange equation one to solve for R the radius of the orbit by using a little bit of algebra. So let's start the rearranging. So R cubed is equal to the period squared multiplied by the gravitational constant multiplied by the mass of the magnetar all divided by four pi square. So now we can plug in plug in all of our known variables to sol for R. So let's do that. So R cubed is equal to the period squared which the period is given to us as the rotation about its axis which was 9.0 seconds square. And the numerical value for the gravitational constant is 6.67 multiplied by 10. The power of negative 11 and its units are newtons multiplied by meters squared divided by kilograms squared. Or I should say newtons multiplied by meters squared per kilogram squared multiplied by the mass of the magnetar, which is 2. multiplied by 10 to the power of kg, all divided by four pi squared. OK. So then R is equal to when we plug all that into a calculator. And we have to note, we have to take everything to a cube square root cubed in order to get the correct answer. So when we calculate and we'll box it in red. So when we plug everything in the red box into our calculator, we should get 3. multiplied by 10 to the power of meters cubed. And note that when we take the cube root of that, we should get our value of R to equal 7.25 multiplied by 10 to the power of 6 m, which is our final answer. Hooray, we did it. So looking at our multiple choice answers, that means the correct answer has to be the letter D 7.25 multiplied by 10 to the power of 6 m. Thank you so much for watching. Hopefully that helped and I can't wait to see you in the next video. Bye.

Verified Solution

Key Concepts

Geosynchronous Orbit

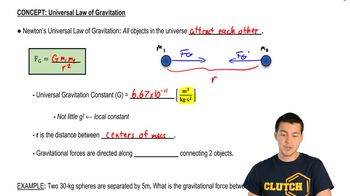
Newton's Law of Universal Gravitation

Centripetal Force