Textbook Question
A 1500 kg car takes a 50-m-radius unbanked curve at 15 m/s. What is the size of the friction force on the car?
518
views
Ch 08: Dynamics II: Motion in a Plane
Chapter 8, Problem 8
A satellite orbiting the moon very near the surface has a period of 110 min. What is free-fall acceleration on the surface of the moon? Astronomical data are inside the back cover of the book.
Verified Solution
Video duration:
1m
This video solution was recommended by our tutors as helpful for the problem above.Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Orbital Period
The orbital period is the time it takes for an object to complete one full orbit around a celestial body. In this case, the satellite's period of 110 minutes indicates how long it takes to circle the moon. This period is crucial for calculating the gravitational force acting on the satellite, which is directly related to the free-fall acceleration experienced on the moon's surface.
Recommended video:
Guided course
04:45
Geosynchronous Orbits
Gravitational Acceleration
Gravitational acceleration is the acceleration experienced by an object due to the gravitational force exerted by a massive body, such as the moon. On the surface of the moon, this acceleration can be determined using the formula derived from Newton's law of universal gravitation, which relates the mass of the moon and the distance from its center to the surface. It is typically denoted as 'g' and varies depending on the celestial body.
Recommended video:
Guided course
07:32Weight Force & Gravitational Acceleration
Newton's Law of Universal Gravitation
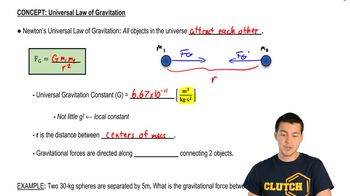
Newton's Law of Universal Gravitation states that every point mass attracts every other point mass in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This law is fundamental for understanding how gravitational forces operate, allowing us to calculate the free-fall acceleration on the moon by relating the satellite's orbital characteristics to the moon's mass and radius.
Recommended video:
Guided course
04:05Universal Law of Gravitation
Related Practice
Textbook Question
A car can just barely turn a corner on an unbanked road at 45 km/h on a dry sunny day. What is the car's maximum cornering speed on a rainy day when the coefficient of static friction has been reduced by 50%?
1216
views
3
rank
Textbook Question
If a vertical cylinder of water (or any other liquid) rotates about its axis, as shown in
FIGURE CP8.72, the surface forms a smooth curve. Assuming that the water rotates as a unit (i.e., all the water rotates with the same angular velocity), show that the shape of the surface is a parabola described by the equation z = (ω^2 / 2g) r^2. Hint: Each particle of water on the surface is subject to only two forces: gravity and the normal force due to the water underneath it. The normal force, as always, acts perpendicular to the surface.
457
views
Textbook Question
Communications satellites are placed in circular orbits where they stay directly over a fixed point on the equator as the earth rotates. These are called geosynchronous orbits. The altitude of a geosynchronous orbit is 3.58 x 10^7 m (approximately 22,00 miles) . Astronomical data are inside the back cover of the book (a) What is the period of a satellite in a geosynchronous orbit?
1677
views
Textbook Question
A 5.0 g coin is placed 15 cm from the center of a turntable. The coin has static and kinetic coefficients of friction with the turntable surface of mu(s) = 0.80 and mu(k) = 0.50. The turntable very slowly speeds up to 60 rpm. Does the coin slide off?
96
views
Textbook Question
a. An object of mass m swings in a horizontal circle on a string of length L that tilts downward at angle θ. Find an expression for the angular velocity ω.
602
views