Standing Waves: Videos & Practice Problems

Standing waves occur when waves interfere in specific patterns, creating nodes and antinodes. The fundamental frequency, denoted as f₁ = v2l, represents the simplest standing wave with one loop. Higher harmonics, or overtones, follow the relationship f_n = n⁢f₁. The wavelength for these waves is given by λ = 2l for the fundamental frequency, illustrating the relationship between frequency, wavelength, and wave speed.

Intro to Transverse Standing Waves

Waves can interact in various ways, and one fascinating outcome of this interaction is the formation of standing waves, particularly in strings. A standing wave appears stationary, despite being the result of two waves interfering with each other. To understand standing waves, consider three scenarios involving a string tied to a fixed point, such as a doorknob.

In the first scenario, when you whip the string up once, a pulse travels to the doorknob. Upon reaching the fixed end, the pulse reflects back inverted. This reflection is a key characteristic of waves at fixed boundaries, where the wave inverts upon reflection.

In the second scenario, if you create two waves by whipping the string up and down twice, the first wave will reach the doorknob and reflect back inverted while the second wave continues moving forward. As these two waves travel towards each other, they interfere, creating a complex pattern. The interference can lead to random wave patterns unless specific conditions are met.

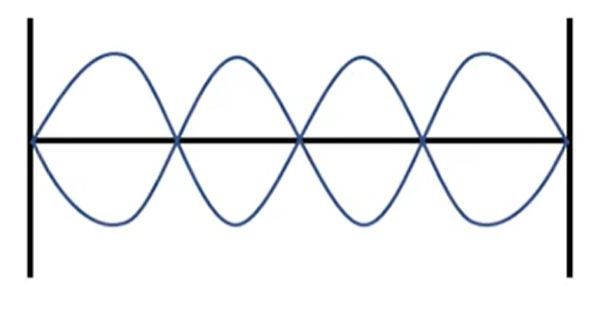
The third scenario introduces the concept of special frequencies. By adjusting the frequency of your hand movements, you can create a standing wave. At certain frequencies, the wave appears to oscillate up and down without moving left or right, resembling a jump rope. This phenomenon occurs because the waves reflect and interfere in such a way that they create nodes (points of no movement) and antinodes (points of maximum movement) along the string.

Standing waves can be characterized by the number of loops, denoted as \( n \). The fundamental frequency, \( f_1 \), corresponds to the simplest standing wave pattern with one loop. The relationship between the frequencies of standing waves is given by the equation:

\[ f_n = n \cdot f_1 \]

where \( f_n \) is the frequency for \( n \) loops. For example, if the fundamental frequency \( f_1 \) is 5 Hz, then the frequency for a standing wave with three loops (\( n = 3 \)) would be 15 Hz, and for five loops (\( n = 5 \)), it would be 25 Hz.

Understanding standing waves is crucial in various applications, including musical instruments and engineering, where wave behavior plays a significant role. By manipulating frequency and observing the resulting patterns, one can gain insights into wave dynamics and resonance phenomena.

By whipping a string up and down, you determine the fundamental frequency to be 4 Hz. If you attached the string to a motorized oscillator and increased the frequency to 28 Hz, how many loops would this standing wave have?

• A. 14
• B. 4
• C. 28
• D. 7

Answer: (D)

One of the harmonic frequencies for a particular string under tension is 325 Hz. The next higher harmonic frequency is 390 Hz. What harmonic frequency is next higher after the harmonic frequency 195 Hz?

• A. 260 Hz
• B. 130 Hz
• C. 196 Hz
• D. 4 Hz

Answer: (A)

Equations for Transverse Standing Waves

Standing waves are formed when waves of the same frequency and amplitude traveling in opposite directions interfere with each other. These waves can only exist at specific harmonic frequencies, which correspond to certain wavelengths. The fundamental frequency, denoted as \( f_1 \), occurs when there is one loop in the standing wave pattern, and it can be calculated using the equation:

$$ f_1 = \frac{v}{2L} $$

Here, \( v \) represents the speed of the wave, and \( L \) is the length of the string. The harmonic frequencies can be generalized as:

$$ f_n = \frac{nv}{2L} $$

where \( n \) is an integer representing the harmonic number (1 for the fundamental frequency, 2 for the first overtone, etc.). The wavelength \( \lambda \) for each harmonic can be derived from the relationship between speed, frequency, and wavelength, given by:

$$ v = \lambda f $$

From this, the wavelength for the \( n \)-th harmonic can be expressed as:

$$ \lambda_n = \frac{2L}{n} $$

For example, consider a string of length \( L = 1.5 \) meters with a wave speed of \( v = 48 \) meters per second. To find the wavelength and frequency of the fundamental tone (where \( n = 1 \)), we calculate:

Wavelength:

$$ \lambda_1 = \frac{2L}{1} = 2 \times 1.5 = 3 \text{ meters} $$

Frequency:

$$ f_1 = \frac{v}{2L} = \frac{48}{2 \times 1.5} = 16 \text{ Hertz} $$

Next, for the first overtone (where \( n = 2 \)), the calculations are as follows:

Wavelength:

$$ \lambda_2 = \frac{2L}{2} = L = 1.5 \text{ meters} $$

Frequency:

$$ f_2 = \frac{nv}{2L} = \frac{2 \times 48}{2 \times 1.5} = 32 \text{ Hertz} $$

Understanding these relationships allows for the determination of both the frequency and wavelength of standing waves in various harmonic states, reinforcing the concept that the overtone frequencies are simply multiples of the fundamental frequency.

The figure below shows a standing wave on a 2.0-m-long string that has been fixed at both ends and tightened until the wave speed is 40 m/s. What is the frequency of this wave?

• A. 20 Hz
• B. 160 Hz
• C. 40 Hz
• D. 10 Hz

Answer: (C)

Example 1

In this example, we analyze a string fixed at both ends, measuring 8 meters in length and having a mass of 0.2 kilograms, subjected to a tension of 100 newtons. To determine the speed of waves on the string, we utilize the formula for wave speed in strings, which is given by:

$$ v = \sqrt{\frac{F_t}{\mu}} $$

Here, \( F_t \) represents the tension in the string, and \( \mu \) is the linear mass density, defined as:

$$ \mu = \frac{m}{L} $$

where \( m \) is the mass of the string and \( L \) is its length. Plugging in the values, we first calculate \( \mu \):

$$ \mu = \frac{0.2 \, \text{kg}}{8 \, \text{m}} = 0.025 \, \text{kg/m} $$

Now substituting \( F_t \) and \( \mu \) into the wave speed equation:

$$ v = \sqrt{\frac{100 \, \text{N}}{0.025 \, \text{kg/m}}} = \sqrt{4000} \approx 63.2 \, \text{m/s} $$

Next, we explore the longest possible wavelength for a standing wave on this string. The longest wavelength corresponds to the fundamental frequency (n = 1), which can be visualized as a single loop. The relationship between the wavelength \( \lambda \) and the length of the string \( L \) is given by:

$$ \lambda_1 = 2L $$

Thus, for our string:

$$ \lambda_1 = 2 \times 8 \, \text{m} = 16 \, \text{m} $$

Finally, we calculate the fundamental frequency using the relationship:

$$ f_1 = \frac{v}{\lambda_1} $$

Substituting the values we have:

$$ f_1 = \frac{63.2 \, \text{m/s}}{16 \, \text{m}} \approx 3.95 \, \text{Hz} $$

In summary, we determined that the speed of waves on the string is approximately 63.2 m/s, the longest possible wavelength for a standing wave is 16 meters, and the fundamental frequency is about 3.95 Hz. These calculations illustrate the relationships between tension, mass, length, wave speed, wavelength, and frequency in the context of standing waves on a string.

A 3m-long rope is stretched between two supports with a tension that makes the speed of transverse waves 60 m/s. What are the wavelength and frequency of the second overtone?

• A. $\lambda=2m;f=30Hz$
• B. $\lambda=1m;f=60Hz$
• C. $\lambda=3m;f=20Hz$
• D. $\lambda=6m;f=10Hz$

Answer: (A)

Here’s what students ask on this topic:

What is a standing wave and how is it formed?

A standing wave is a wave pattern that results from the interference of two waves traveling in opposite directions. It appears to be stationary, with nodes (points of no displacement) and antinodes (points of maximum displacement). Standing waves are formed when the frequency of the waves matches the natural frequency of the medium, creating constructive and destructive interference at specific points. This can be observed in strings, air columns, and other mediums where waves can reflect and interfere.

What is the fundamental frequency in standing waves?

The fundamental frequency, denoted as f₁, is the lowest frequency at which a standing wave can form in a given medium. It corresponds to the simplest standing wave pattern with one loop (or one-half wavelength) along the medium. The fundamental frequency is given by the equation:

$f$₁=v2l

where v is the wave speed and l is the length of the medium.

How do you calculate the wavelength of a standing wave?

The wavelength of a standing wave can be calculated using the relationship between the wave speed (v), frequency (f), and the length of the medium (l). For the fundamental frequency (n=1), the wavelength (λ) is given by:

$\lambda =\frac{2l}{n}$

where n is the harmonic number. For higher harmonics, the wavelength is divided by the harmonic number (n).

What are harmonic frequencies in standing waves?

Harmonic frequencies are the frequencies at which standing waves can form in a medium, corresponding to different numbers of loops (or nodes and antinodes) along the medium. The fundamental frequency (f₁) is the first harmonic, and higher harmonics are integer multiples of this frequency. The nth harmonic frequency (f_n) is given by:

$f$_n=nf₁

where n is the harmonic number (1, 2, 3, ...).

How do you determine the speed of a wave in a string?

The speed of a wave in a string can be determined using the relationship between the wave speed (v), the tension in the string (T), and the linear mass density (μ) of the string. The wave speed is given by:

$v=\sqrt{\frac{T}{\mu }}$

where T is the tension in the string and μ is the mass per unit length of the string.