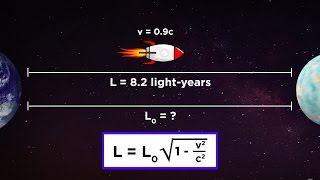35. Special Relativity
Consequences of Relativity
Learn with other creators
Practice this topic
- Multiple Choice
The international space station travels in orbit at a speed of 7.67 km/s. If an astronaut and his brother start a stop watch at the same time, on Earth, and then the astronaut spends 6 months on the space station, what is the difference in time on their stopwatches when the astronaut returns to Earth? Note that 6 months is about 1.577 x 107 s, and c = 3 x 10 8 m/s.
431views2rank2comments - Multiple Choice
In the following figure, a right triangle is shown in its rest frame, S'. In the lab frame, S, the triangle moves with a speed v. How fast must the triangle move in the lab frame so that it becomes an isosceles triangle?
405views1rank1comments - Multiple ChoiceCarol is in the same reference frame with a clock. Bianca is flying past Carol and her clock at a high speed. Bianca sees Carol's clock ticking at one quarter the rate that Carol sees. How fast is Bianca flying relative to Carol?333views
- Multiple ChoiceCarl is standing in a park 1000 m across. Rohan flies over the park at a very high speed, first passing over the east end of the park, and then passing over the west end. Carl and Rohan are discussing the time interval between when Rohan passed over the east end of the park and when he passed over the west end of the park. Who measured the proper time?304views
- Textbook QuestionBjorn is standing at x = 600 m. Firecracker 1 explodes at the origin and firecracker 2 explodes at x = 900 m. The flashes from both explosions reach Bjorn's eye at t = 3.0 μs. At what time did each firecracker explode?173views
- Textbook Question
(II) Two identical black holes form a binary system and are orbiting one another. Assume they are a distance apart which is twice the Schwartzchild radius in each. Then, assuming Newton mechanics is still valid, how fast are they moving with respect to the center of mass?
183views - Textbook Question
(III) A certain atom emits light of frequency ƒ₀ when at rest. A monatomic gas composed of these atoms is at temperature T. Some of the gas atoms move toward, and others away from, an observer due to their random thermal motion. Using the rms speed of thermal motion, (a) show that the fractional difference between the Doppler-shifted frequencies for atoms moving directly toward the observer and directly away from the observer is ∆ƒ/ƒ₀ ≈ 2 √3kT/mc². Assume mc² ≫ 3kT. (b) Evaluate ∆ƒ/ƒ₀ for a gas of hydrogen atoms at 650 K. [This “Doppler-broadening” effect is commonly used to measure gas temperature, such as in astronomy.]
127views - Textbook QuestionA rocket ship flies past the earth at 91.0% of the speed of light. Inside, an astronaut who is undergoing a physical examination is having his height measured while he is lying down parallel to the direction in which the ship is moving. (a) If his height is measured to be 2.00 m by his doctor inside the ship, what height would a person watching this from the earth measure? (b) If the earth-based person had measured 2.00 m, what would the doctor in the spaceship have measured for the astronaut’s height? Is this a reasonable height?158views