A quantum particle has energy levels in a 1D box of length 0.87 nm: E _n = 12.5 eV and E _n+1 = 18.9 eV. Find the particle's mass and also identify the particle.

Evenly distributed free protons occupy the range 0 ≤ y ≤ 5 m. No protons are detectable outside this range. Calculate the probability density at y = 2.5 m.

Consider an unstable atomic nucleus that experiences alpha decay and releases 6.05 MeV energy. When the mass of the parent nucleus and the resulting daughter nucleus are added together, it amounts to 420 u. Can you determine the original parent nucleus mass before it decayed?

Suppose two neon atoms (²⁰Ne) combine to form a calcium atom (⁴⁰Ca); how much energy is emitted? The binding energy per nucleon in ²⁰Ne and ⁴⁰Ca is 8.0 MeV and 8.6 MeV respectively. 

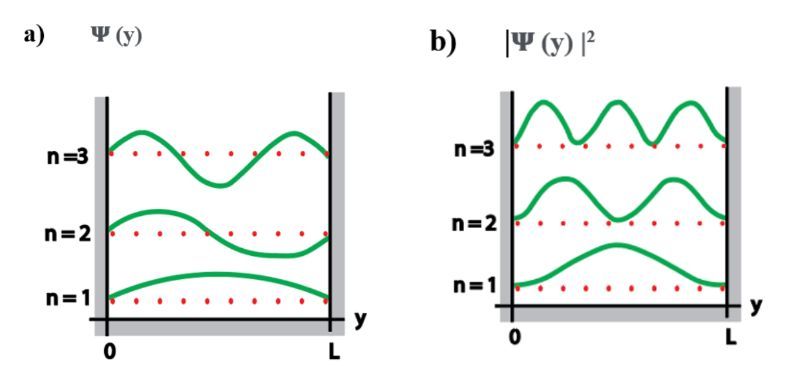
The probability of detecting a particle with a normalized wave function ψ(y) within the limits of y and y + dy is given by (|ψ|²)dy. The normalized wave function for a particle in a box with boundaries at y = 0 and y = L is ψ_n(y)=√(2/L)•sin⁡[(nπy/L)]. The possible values of n are n = 1,2,3... Assuming the particle to be in the ground state, i) At which values of y in the range 0 ≤ y ≤ L the particle is impossible to be found? ii) At which values of y within the boundary the particle is most likely to be found? iii) Do your values agree or differ with these curves?

The wave function ψ(x,t) = A[e^{i(2kx - 4ωt)} - e^{i(4kx - 16ωt)}] describes a particle oscillating in a one-dimensional path. Constants k and ω are real and positive. Determine v_av using the approach where v_av is the ratio of the distance moved by the maxima divided by the change in time. Hint: Use values of t in the form nπ/ω.

A cube of length 2.5 cm is confined in a one-dimensional space given by y = 0 to y = 80 cm. The cube bounces back and forth in the boundaries of this space. The magnitude of the velocity remains constant before and after bouncing. At an arbitrary instant, determine the probability that the cube's center lies in the range 38 cm ≤ y ≤ 42 cm.