One-Time Games and the Prisoner's Dilemma - Online Tutor, Practice Problems & Exam Prep

Game Theory, One-Time Games, and the Prisoner's Dilemma

Alright, you guys ready to have some fun? We're about to learn about games. So in an oligopoly, what we're gonna see is that they have to work strategically to make their pricing decisions because there's only a few firms and it makes a big difference what your competitors are doing in these markets. In other markets we were dealing with the idea of marginal revenue equals marginal cost to find the profit-maximizing quantity, well that's why I said this one's kind of like an odd one out. We're going to be dealing with it through this game theory, alright? Let's check it out. So game theory, this is one where making decisions and the outcomes depend on the interaction with others, okay? So we're going to be thinking about what other people are doing when we make our decisions, okay? So the first type of game we're going to talk about is a one-time game, alright? A one-time game is a game that gets played one time. Who would have thought, right? So let's go right into our example. This is the prisoner's dilemma. This is one of the most famous examples of a one-time game and it's pretty much always used to introduce students to game theory. Okay? So you're gonna see what happens here in the prisoner's dilemma. So let's scroll down a little bit and let's see what we get. Alright, we've got Bad Boy Benny and Evil Eddie were recently arrested after some casual B and E. If you weren't raised by the streets like me, B and E, that's a little breaking and entering, Just a little Friday night fun, right? The police do not have enough evidence to make a strong case against them, but can nail them for smaller crimes. So after being separated into separate into different cells, that's key, right? They're separated into different cells. They're not able to communicate with each other, okay? The police make each prisoner the same offer. Okay, so this is important right here. This next sentence, these are gonna be the payoffs of the game, right? This is where all of our information pretty much comes from. Right now, we can lock you up for a year. That's what they tell the prisoner, right? Right now, we can lock you up for a year. If you confess, we will let you go free and your partner will get 20 years, but if you both confess then you're each gonna get an 8-year sentence, right? So this is a pretty case, right? Because now they have to think oh is my partner going to confess? Are they not going to confess, right? How am I going to get the best sentence that I can get? Alright, so to funnel all this information and make it easy to take in, we build what's called a payoff matrix, okay? And it's gonna look something like this. We're gonna have bad boy Benny's decisions going down, he can either confess or not confess and then we've got evil Eddie's decisions. He can either confess or not confess. Right? So this is a payoff matrix and it's still empty. Let's go ahead and fill it in. Alright? This is our payoff matrix, so let's go 1 by 1 here. Let's start with this first sentence. Right now, we can lock you up for a year. So this doesn't even matter, if you don't confess, we're gonna lock you up for a year, right? So if both partners don't confess, if I don't confess or Bad Boy Benny doesn't confess and Evil Eddie doesn't confess, they're gonna each get 1 year, right? So what we're gonna do is we're gonna go to this box where it's don't confess and don't confess for both of them and we're gonna put on their payoffs. So I'm gonna put b for bad boy Benny. He would get 1 year if they both don't confess. Right? How about Evil Eddie? If they both don't confess, they're gonna nail him for the smaller crimes and they are gonna get 1 year each. Right? Excuse me. Alright. So how about our next sentence? If you confess, we will let you go free and your partner will get 20 years. Okay, so this is a situation where one person confesses and the other one doesn't confess, okay? So let's say that bad boy Benny doesn't confess and evil Eddie does confess. Well if evil Eddie is the confessor, right? Bad boy Benny will get 20 years in prison, right? Evil Eddie ratted him out and bad boy Benny gets 20 years in prison and evil Eddie right here, evil Eddie will get 0 years, right? He's gonna go scot-free. If he confesses while bad boy Benny doesn't confess. Now it's the same thing the other way around, right? If bad boy Benny is the confessor and evil Eddie doesn't confess, well in that case bad boy Benny is the confessor and bad boy Benny right down here, right where bad boy Benny confesses in this column and Evil Eddie doesn't confess in the bottom row, well Bad Boy Benny for confessing he's gonna get get 0 years, right? And evil Eddie will end up spending 20 years in prison there. Wow. That sounds awful. Alright, how about the last case, right? In this last sentence they say if you both confess, you each get an 8-year sentence. So if they both decide to confess, they're gonna each get 8 years, right? So Bad Boy Benny, if they confess and confess would get 8 years and Evil Eddie will also get 8 years. Alright? So that's how we set up our payoff matrix. Now we have all our information in one place, the next thing to do is decide what is each person's best decision, alright? So let's pause here and in the next video we'll continue by solving this prisoner's dilemma, alright? Let's do that now.

Dominant Strategy and the Nash Equilibrium

Alright, so before we check what our best situation is, let's go down here and think about our dominant strategy. So, to make our best decision, what we want to do is think about what we would do in response to each of our opponent's decisions, right? So what would Bad Boy Benny want to do if Evil Eddie decides to confess? Or what would Bad Boy Benny want to do if Evil Eddie decides not to confess, right? We want to see what our best scenario is based on our opponent's decisions, right? This is the interdependence that we see happening, okay? And we're going to say that a dominant strategy is your best strategy regardless of what the other player does. So, you could have a dominant strategy which would be a situation where whether Eddie confesses or doesn't confess, it's going to make more sense for me to confess no matter what, right? That would be a dominant strategy where you would do the same thing regardless of the other person's decisions. And I just want to make sure that you understand that not every game has a dominant strategy and also not every player. Sometimes one player will have a dominant strategy and the other one doesn't. Sometimes they both do, sometimes nobody does, right? So, a dominant strategy is only when you have one best option overall. Okay, so let's go now to our payoff matrix and let's think about what each person's best decision could be in each case. Let's start with Bad Boy Benny's decisions. Okay? So for Bad Boy Benny to decide what his best choices are, he has to think about what Evil Eddie would do. So, the first hypothetical would be for Bad Boy Benny to think, okay, what would I do if Evil Eddie were to confess? Okay, so if Evil Eddie were to confess, I have the option to confess and get 8 years, right? Up here. If Evil Eddie is for sure confessing, I can either confess and get 8 years or not confess and get 20 years, right? So, if the situation is that Evil Eddie is going to confess, it makes more sense for Bad Boy Benny to confess, right? He's going to get 8 years instead of 20 years, so I'm going to circle this right here, okay? Bad Boy Benny would be best off confessing if Evil Eddie confesses. Now, what if Evil Eddie doesn't confess? Let's think what would be Bad Boy Benny's best decision. Well, if Evil Eddie's not going to confess, Bad Boy Benny is either going to get 0 years, right? He's going to go free if he confesses or he'll get 1 year where they both don't confess, keep their mouths shut, and they just get pegged for the 1 year each. Each. Okay, so in this situation, it makes more sense for Bad Boy Benny to confess again, right? It makes more sense for him to confess because he's going to go scot-free, he spends less time in jail, so in his best interest it would be better to confess, right? 0 years in prison would be his better choice. So you can already see that for Bad Boy Benny, his dominant strategy is going to be to confess, right? Because whether or not Evil Eddie confesses or doesn't confess, Bad Boy Benny gets a lower sentence by confessing, okay? Let's do the same thing now with Evil Eddie's decisions. So first, Evil Eddie has to think what would I do if Bad Boy Benny confesses? So if Bad Boy Benny confesses, Evil Eddie well he has to choose between 8 years by confessing where they both ride each other out or not confessing and Bad Boy Benny would go free, but he would get 20 years, right? So Bad Boy Benny confesses, it makes more sense for Evil Eddie to confess, right? He'd rather spend 8 years than 20 years in prison. How about the other one? If Bad Boy Benny decides not to confess, what's Evil Eddie's best decision? Well, he has to choose between 0 years and 1 year, right? By confessing, he can go scot-free, but by not confessing, he would spend 1 year in prison. So his best option again is to confess and this is the prisoner's dilemma because both of them have a dominant strategy to confess, right? So it's in their best interest personally to confess, but what we see is that that's a bad thing overall, right? Because they're both going to confess and they're both going to end up at 8 years in prison, which is not ideal, right? We would probably think more ideal at least would be this box, right? Where they both don't confess at least instead of 8 years each, they're only getting 1 year each, right? So we would think that that box is where they would want to be, but since they can't talk to each other, they're not going to be able to make that decision and they're going to end up confessing, at least that would be their best choice, right? So what we call this situation where they both end up in the same place, this is called the Nash equilibrium. Nash, so this guy Nash, he's a famous economist who discovered this idea about game theory, about this Nash equilibrium. They made this excellent movie, there was a book written about his life called A Beautiful Mind. If you haven't seen it, it's a great movie whether or not you love economics or not, and I would suggest it. He won a Nobel Prize for these ideas, so this is what he thought here. The Nash equilibrium is going to occur where all players are making their best choice, so they're all making their best choice, which in this case was for each to confess, right? They're making their best choice given their competitors' options, right? So that Nash equilibrium is where they're both making their best choice and that was confess and confess, right? So, the Nash equilibrium would be this box up here that I'm going to circle in green, the confess confess box, right? The confess confess box is our Nash equilibrium, okay? But notice that it's not the best situation, right? We've been talking about equilibriums in this class and equilibrium was usually a good thing, right? Equilibrium was where we were being efficient this and that, but in game theory, the equilibrium does not necessarily mean it's the best outcome for all the players, right? It's just where they're all making their best decisions and this is where we end up, okay? So it's not necessarily the best outcome, it's where we're going to end up if everyone's just making their best decisions. So that's unfortunate, right? They're both going to end up spending 8 years in prison, but they could possibly have had a different situation if they could cooperate. Right? So let's pause here and in the next video, let's discuss cooperation.

Collusion, Cartels, and Price Leadership

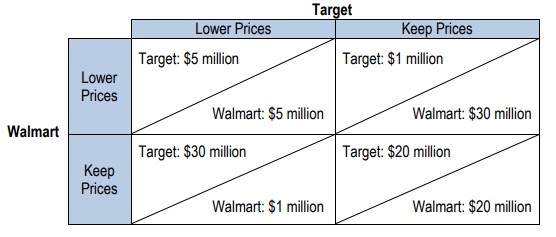
Alright, so let's continue here on the bottom part of the page. So in this game, both players would have been better off, right? They could have been better off if they could have discussed with each other, hey let's both keep our mouth shut and we'll only get 1 year in prison, right? If they could cooperate and both don't confess, they would have been in a better place, right? They would have had only 1 year each instead of 8 years each, right? So what do we call this, right? Now let's extend this to the idea of the oligopoly, right? Here we were just talking about the prisoner's dilemma, let's see how this relates in the big sense. Well, when we think about this with firms, this could be firms colluding together. We're going to think of this idea of collusion where they work together to set prices, right? So it's an agreement between the firms to set their quantities and price, okay? So that's called collusion where they're working together and that's illegal in the United States. Competing firms are not allowed to explicitly talk about pricing or quantity, right? It's not like McDonald's can call Burger King and say, hey, let's raise our prices of burgers and everyone's going to charge $3 for burgers or Coke calling up Pepsi and saying, hey no longer are we going to sell 20 ounces for a dollar, 20 ounces are going to be $4 now, okay? That's not allowed. That's illegal in the US because it's reducing competition okay? So what we call firms that are colluding is called a cartel. Okay, a cartel is firms that are colluding together. The group colluding together is a cartel. A very famous cartel is OPEC. So OPEC is a group of Middle Eastern nations that get together and set prices and quantities that they're going to put for oil, right? They control a lot of the world's oil and they limit the quantity so that they can inflate the price, okay? That would be illegal in the United States, but they're not in the United States so they can do whatever they want over in their country, okay? So OPEC is an existing cartel, but what we're going to see in situations where people are colluding and where we have cartels is that there's an incentive to cheat, to increase their individual profits. I'm going to put individual profit up here, okay? So you could cheat when you know other people are going to cooperate, right? So the idea is this cartel, they all cooperate on what quantity they're going to produce, but then you have that information, you know what everyone's going to produce and you have that incentive to cheat and produce a little extra to make more money or something like that. So let's think about this idea of Cartel in our situation up here, right? If they had gotten together and they were able to collude together to say, hey let's both not confess, right? If we both don't confess we only get 1 year instead of the 8 year equilibrium. They're obviously both very smart at game theory and have been through this class before. Alright, so they think they could collude and they'll each get 1 year. But let's think about that incentive to cheat. Now Bad Boy Benny, after this discussion with Evil Eddie, knows that Evil Eddie is planning to not confess, right? So if Evil Eddie is planning to not confess, Bad Boy Benny could cheat and confess, right? He could confess and he could go free. We could be in the situation where Evil Eddie doesn't confess and Bad Boy Benny takes advantage of it, confesses, Bad Boy Benny is gone. 0 years in prison, Evil Eddie gets 20 years and Bad Boy Benny is better off, right? He increased his individual profit, right? His own profit which was less time in prison by cheating, cool? So there's that incentive to cheat when you know that other people are going to cooperate. So the last thing here is an idea of implicit collusion, okay? So price leadership is not illegal in the United States, it might be a bit unethical, but the idea here is where we're going to have one firm taking the role of the price leader, okay? So it's a form of collusion where one firm announces a price, so let's say there's a new video game system, right? And it's like the PS12 or whatever and the PS12 comes out and Walmart announces, we are selling PS 12s for $500 right? And then you see Target's $500 Toys R Us $500 Everybody's selling the PS 12 for $500 right? And that's because of this price leadership situation, right? The first firm announced the price and everyone followed suit because they knew that they could make more money if they all charge the same higher price and increase their profit, okay? So this is not illegal because you're not really colluding, you're just saying hey, they're charging 500, I'm going to charge 500. We didn't talk about this at all, it just seems like the right price to me, right? So you could see how there could be some gray areas there. Right, price leadership that's a form of implicit collusion. Cool? Let's go ahead and move on to the next video now.

One-Time Games:Finding Dominant Strategies and Nash Equilibrium with the "Check and X"Method

Alright guys, now I want to show you an easy method, and this is the method I use when solving payoff matrices and using game theory, okay? So what this helps us do is it helps us find our dominant strategies and it helps us find Nash equilibriums, okay? So what I call this method, it's something like the check and X method, right? Kind of a weird name, but the check and X method is what it is and these are the steps we're going to do. First, we're going to put a check next to each of player 1's best strategies and put an X for each of player 2's best strategies, okay? So that's all we have to do. Just the checks and the X's and then we're going to analyze our solutions, okay? So let's go ahead and do the checks and X's and then we'll see how our solutions work.

Okay, so let's go down to this example. Notice we didn't even need to be given a story in this case, right? They didn't have to tell us this whole backstory, they just threw payoffs at us, right? They told us in this case you're going to get $300 in this case $500, right? They just threw numbers, we don't need a whole backstory, the payoff matrix can just be filled in like this, okay?

So let's go ahead and start with player 1's best decisions, right? We want to see what's player 1's best strategy, should he choose option A or choose option B, okay? So let's go ahead and start here. Remember that to pick your best strategy, you have to decide what you would do in each case of your competitors' choices. Alright, so for player 1's first choice, they have to decide what would I do if player 2 chooses A, right? If player 2 chooses A, player 1 can choose A and get $300, or player 1 can choose B and get $400. Right? So you can see that if player 2 chooses A, player 1 will want to choose B. So we're going to put a check down here in this box because that is player 1's best strategy in that case.

Now what if player 2 chooses B? If player 2 chooses B, player 1 can choose A and get $100 or they can choose B and get $200. So, again, B is going to be their best strategy, okay? So before we make our conclusions, let's do the other thing. Let's do the X's with player 2's decisions. Alright, so the opposite. Now player 2 has to think, what would be best if player 1 chooses A, what's my best choice? So player 1's going to choose A, so we have to look in this row right here. Player 2 can either choose A for $500 or player 2 can choose B for $400. So player 2 is going to choose A, right? A gets them more money so they choose A when player 1 chooses A. Now what if player 1 chooses B? What is player 2's best strategy? Well, player 2 could either get $100 if player 1 chooses A or player 2 can get $200, right?

That's behind me. Right? Player 2 could either get the $100 down here or the $200, so they're going to pick the $200, right? So what we're going to do is we're going to put an X in this box as well. So notice that this box in the bottom right has a check and an X in it, and then there's a check in this box and an X in that box up there, and then the box, player 1 choosing A, player 2 choosing B has nothing in it, okay?

So now let's go to our analyze our solution up here. Step 3. So the first thing we want to do is check if there's any row or any column that has both checks or both X's, alright? So what we see is that we have checks and checks in this row, right? There's a row with checks, but the X's are not in a column, right? The X's are diagonal. So this is not okay. This diagonal with the X's, that does not give us our answer. Okay? So what we do know is that player 1 has a dominant strategy, right, because the checks are for player 1 and player 1 has a row with both of the checks, right? So both of the checks are in the B row, so for player 1, the dominant strategy is to choose B, okay?

So let's go down here. Player 1's dominant strategy is B, right? And that's because those checks are both in that row. What about player 2's dominant strategy? Well, player 2, we saw that the X's are not in the same column at all, right? There's an X in column A and an X in column B, so they'd have no dominant strategy, right? So I told you that there could be situations where you might not have a dominant strategy. Well, here's one, right? He's going to choose A in one case and B in the other case. So last but not least, let's discuss Nash equilibriums, and that's here in B. Remember that a Nash equilibrium is where both players are making their best decisions based on their opponent's decisions, okay? So what we're going to see is that any box that has both a check and an X, so if there's a box with a check and an X in it, that is a Nash equilibrium, okay?

And what do we have right here behind me? We've got that bottom right box with both a check and an X, okay? So that is going to be our Nash equilibrium right there and that would be basically the situation where we're probably going to end up. If everyone's acting rationally, we're going to end up in a situation where both player 1 and player 2 get $200, okay? So Nash Equilibrium is, I'm going to put it in a bracket here, B, B, right? Where they both choose B. I don't think that's like proper writing etiquette with it, but that's just the idea, right? They're both choosing B and that is the Nash equilibrium. Alright? So let's see. Is there anything else here? Nope. That’s about it for this lesson, right?

I just wanted to teach you how to use that check and X method. Okay? So let's go ahead and move on to the next video. Let's get some practice using this method.

Based on the information in the payoff matrix, which of the following is true? 

• A. This situation is not a prisoner's dilemma
• B. If Walmart lowers its price, Target should keep its prices high
• C. If Target lowers its price and Walmart does not, Target will earn $20 million economic profit
• D. Both Walmart and Target would jointly be better off if they could each keep their prices high

The game above has: 

• A. A Nash equilibrium:both Walmart and Target keep prices high
• B. A Nash equilibrium:both Walmart and Target lower prices
• C. A Nash equilibrium:Target keeps prices high and Walmart lowers prices
• D. No Nash equilibrium

In a cartel, the incentive to cheat is significant because

• A. Each firm has an incentive to decrease its own output
• B. Each firm has an incentive to raise its price
• C. Each firm has an incentive to expand its output
• D. Each firm's marginal cost exceeds the price that the cartel sets

Here’s what students ask on this topic:

What is the Prisoner's Dilemma in game theory?

The Prisoner's Dilemma is a fundamental concept in game theory that demonstrates why two rational individuals might not cooperate, even if it appears that it is in their best interest to do so. In this scenario, two prisoners are arrested and interrogated separately. They can either confess or remain silent. If both confess, they receive moderate sentences. If one confesses and the other remains silent, the confessor goes free while the silent prisoner gets a heavy sentence. If both remain silent, they receive light sentences. The dilemma shows that individual rationality leads to a worse collective outcome.

What is a dominant strategy in game theory?

A dominant strategy in game theory is a strategy that yields a better outcome for a player, regardless of what the other players do. In other words, it is the best course of action for a player no matter what the opponents' strategies are. For example, in the Prisoner's Dilemma, confessing is a dominant strategy for both prisoners because it results in a better personal outcome whether the other prisoner confesses or not. Not all games have dominant strategies, and sometimes only one player may have a dominant strategy.

What is Nash Equilibrium in the context of the Prisoner's Dilemma?

Nash Equilibrium, named after John Nash, is a concept in game theory where each player's strategy is optimal given the strategies of the other players. In the context of the Prisoner's Dilemma, the Nash Equilibrium occurs when both prisoners choose to confess. This is because confessing is the best response for each prisoner, given that the other prisoner might also confess. Although this leads to a suboptimal outcome (both getting 8 years in prison), it is the stable state where neither prisoner can improve their situation by unilaterally changing their decision.

How does the concept of collusion relate to the Prisoner's Dilemma?

Collusion in the context of the Prisoner's Dilemma refers to the idea that if the prisoners could communicate and agree to both remain silent, they would achieve a better collective outcome (each getting only 1 year in prison). This mirrors how firms in an oligopoly might collude to set prices or output levels to maximize joint profits. However, just like in the Prisoner's Dilemma, there is an incentive to cheat on the agreement to gain individual advantage, which can undermine the collusion and lead to worse outcomes for all parties involved.

What is the significance of the payoff matrix in game theory?

The payoff matrix is a crucial tool in game theory that organizes the potential outcomes of a game for each combination of strategies chosen by the players. It helps in visualizing and analyzing the payoffs for each player based on their decisions and the decisions of others. In the Prisoner's Dilemma, the payoff matrix shows the sentences each prisoner will receive based on whether they confess or remain silent. This matrix is essential for identifying dominant strategies and Nash Equilibria, aiding in the understanding of strategic interactions and decision-making processes.