Chapter 2, Problem 80
Use the mass spectrum of rubidium to determine the atomic mass of rubidium.
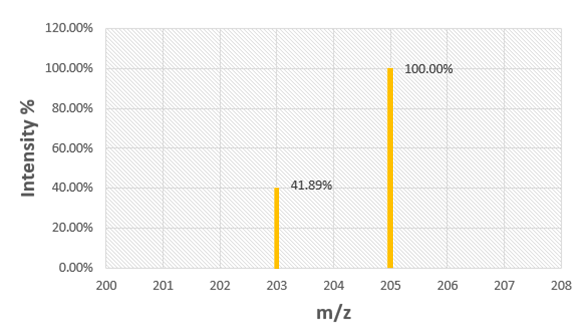
 Verified Solution
Verified SolutionVideo transcript
Bromine has two naturally occurring isotopes (Br-79 and Br-81) and has an atomic mass of 79.904 amu. The mass of Br-81 is 80.9163 amu, and its natural abundance is 49.31%. Calculate the mass and natural abundance of Br-79.
Silicon has three naturally occurring isotopes (Si-28, Si-29, and Si-30). The mass and natural abundance of Si-28 are 27.9769 amu and 92.2%, respectively. The mass and natural abundance of Si-29 are 28.9765 amu and 4.67%, respectively. Find the mass and natural abundance of Si-30.
Use the mass spectrum of europium to determine the atomic mass of europium.
How many sulfur atoms are there in 5.52 mol of sulfur?
How many moles of aluminum do 3.7 * 1024 aluminum atoms represent?
What is the amount, in moles, of each elemental sample? a. 11.8 g Ar
