A solution of a nonvolatile solute in water has a boiling point of 375.3 K. Calculate the vapor pressure of water above this solution at 338 K. The vapor pressure of pure water at this temperature is 0.2467 atm.
Find the mass of urea (CH4N2O) needed to prepare 50.0 g of a solution in water in which the mole fraction of urea is 0.0770.

Verified Solution
Key Concepts
Mole Fraction
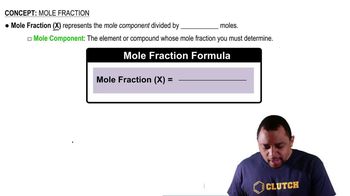
Molar Mass

Mass Percent and Solution Preparation

The density of a 0.438 M solution of potassium chromate (K2CrO4) at 298 K is 1.063 g/mL. Calculate the vapor pressure of water above the solution. The vapor pressure of pure water at this temperature is 0.0313 atm. (Assume complete dissociation of the solute.)
The vapor pressure of carbon tetrachloride, CCl4, is 0.354 atm, and the vapor pressure of chloroform, CHCl3, is 0.526 atm at 316 K. A solution is prepared from equal masses of these two compounds at this temperature. Calculate the mole fraction of the chloroform in the vapor above the solution. If the vapor above the original solution is condensed and isolated into a separate flask, what will the vapor pressure of chloroform be above this new solution?
A solution contains 10.05 g of unknown compound dissolved in 50.0 mL of water. (Assume a density of 1.00 g/mL for water.) The freezing point of the solution is -3.16 °C. The mass percent composition of the compound is 60.97% C, 11.94% H, and the rest is O. What is the molecular formula of the compound?
The osmotic pressure of a solution containing 2.10 g of an unknown compound dissolved in 175.0 mL of solution at 25 °C is 1.93 atm. The combustion of 24.02 g of the unknown compound produced 28.16 g CO2 and 8.64 g H2O. What is the molecular formula of the compound (which contains only carbon, hydrogen, and oxygen)?
A 100.0-mL aqueous sodium chloride solution is 13.5% NaCl by mass and has a density of 1.12 g/mL. What would you add (solute or solvent) and what mass of it to make the boiling point of the solution 104.4 °C? (Use i = 1.8 for NaCl.)
