The vapor pressure of CCl3F at 300 K is 856 torr. If 11.5 g of CCl3F is enclosed in a 1.0-L container, will any liquid be present? If so, what mass of liquid?
A sealed flask contains 0.55 g of water at 28 °C. The vapor pressure of water at this temperature is 28.35 mmHg. What is the minimum volume of the flask in order that no liquid water be present in the flask?
 Verified step by step guidance
Verified step by step guidance
Verified Solution
Key Concepts
Vapor Pressure
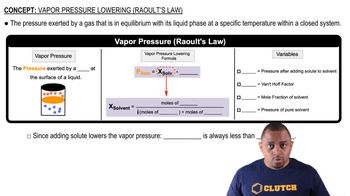
Ideal Gas Law

Molar Mass and Moles

A sample of steam with a mass of 0.552 g and at a temperature of 100 °C condenses into an insulated container holding 4.25 g of water at 5.0 °C. Assuming that no heat is lost to the surroundings, what is the final temperature of the mixture?
Air conditioners not only cool air, but dry it as well. A room in a home measures 6.0 m × 10.0 m × 2.2 m. If the outdoor temperature is 30 °C and the partial pressure of water in the air is 85% of the vapor pressure of water at this temperature, what mass of water must be removed from the air each time the volume of air in the room is cycled through the air conditioner? (Assume that all of the water must be removed from the air.) The vapor pressure for water at 30 °C is 31.8 torr.
Based on the phase diagram of CO2 shown in Figure 11.39(b), describe the state changes that occur when the temperature of CO2 is increased from 190 K to 350 K at a constant pressure of (a) 1 atm
