What is the mole fraction of oxygen gas in air (see Table 5.3)? What volume of air contains 10.0 g of oxygen gas at 273 K and 1.00 atm?

Video transcript

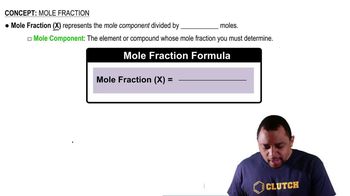
Alright, So in this practice problem, we are going to have to uh to questions so we need to calculate mole fraction Of oxygen in the air. So here we have composition of of dry air and we're going to be looking at the oxygen and were given percent by volume for the oxygen. And then the second question, if air contains 18 g of oxygen gas at that temperature and at that pressure, what is the volume of air? Not volume of oxygen by volume of air. So like the total everything. Right? So let's just take a look at the first one. Alright, so we want mole fraction. And remember mole fraction. So here, oxygen gas of 02, that would just equal two moles of 02 divided by the total moles. Right? But we don't really have moles. We have percentages here by volume and we know that moles number of moles and volume are actually directly proportional to one another according to avocados law. Right? So if we take a look at these percent by volume, Well, the 1%. So 21%. It's just going to mean that there's 21 L of 02 Per 100 l Volume of this air, right? And then Times 100. And that's why we get 21%. But for mole fraction, if we say that, you know these these volumes, we can treat the most moles, we can say that um you know that there's going to be 21 L per 100 per 100 liter. That means that there's actually 0.21 moles per one mole of air. Right? So that's going to equal to 0. moles of air For every one mole of this dry air. Okay, Because here, we're not actually looking at the percentage, So we're just dividing 21 by 100 which would give us 1000.21 because this is not percentage. We wouldn't be multiplying it by 100. That's why it's 1000.21 not 21. Okay, so actually mull fraction here is just 210.21. Right, So that is the mole fraction of oxygen gas here. Alright, so if we take a look at the second question, they want the volume of this whole air that contains everything including the oxygen, if it contains this much grams of oxygen. So, because this is all that's kind of given to us and we we can't use the ideal gas law equation just yet, because we do need to find out how many moles of air we have, we're going to be able to find molds of air from grams of oxygen and then moles of oxygen. two moles of air. Okay, so once we have moles of air, we can find Um the volume of air by using ideal gas law equation. So let's go ahead and take the 18g of oxygen that we have. And first we're going to convert that into moles. So in one mole of 02 oxygen weighs g, there are two of them. So this would be 32 g of oxygen. Alright, so that would be moles. And now we can do a basically multiple comparison because we already found the mole fraction. And we said that for uh you know, for every one mole of air there's .21 moles of 02. So this is actually the conversion factor that we're going to be using. So .21 moles of oh, to go on the bottom because we want them to cancel out. And then for every one mole of air. Alright, so this will give us smalls of air. Let's go ahead and calculate that. And that will be 2. moles of air. So that is the total mole of air that we have here Um in this, in this mixture that contains 18 g of oxygen. So now that we have these N we can look at the ideal gas law equation and what do we need to solve for for the volume? Right. Because pressure here is given to us in atmospheres uh molds. We just found r as a gas constant, we always have that. And temperature is also given to us in the correct units of Calvin. So let's go ahead and solve for the volume. We're gonna divide both sides by by pressure. So N R. Etc overpressure Moles is right here, 2. R is the gas constant .08 to six liters. Times atmospheres over more times Calvin. Okay. And then times the temperature. What was that again to 85 Calvin 285 Calvin. And then everything divided by the pressure. And then the total pressure we were told is 1.20 atmospheres. Alright, so all let's see moles cancel with moles, atmospheres with atmospheres, Calvin's with Calvin's. And we're going to have leaders left over. And that makes sense because we are solving for the volume. So this would be the total volume of air, right? Because we're using M.olds of the total air. So let's go ahead and multiply and then divide and our finally answer for the second problem would be 52.2 L. Alright, so we are done here. So let's go ahead and go over what we did here. So for the first question we wanted mole fraction of oxygen. Of course we didn't have moles what we could we basically figured out how many moles we had of 02 per one mole of air by using the percent by volume. Because here we said that and you know, for every 100 liter air we have 21 liters of oxygen. That's what that 21% means. But because mole fraction is not percentage. If we say that volume here is proportional to two moles, it becomes 21 moles divided by moles of air would give us .21 moles or 0.21 for the mole fraction. Which means that there are 0.21 miles per one mole of air in total. Right? So that is how we found the mole fraction of oxygen by using the percent by volume. And then to find the volume of air, which is, you know, the whole thing that we have here, we were given some information on oxygen how much we had. So we took that converted to moles, then found moles of air by using the mole fraction that we found in the first question. And that gave us the moles of air. And then we just plugged that into the ideal gas law equation, assault for the only other variable that was unknown which was volume. Okay, Alright folks, we're done. Please let us know if you have any questions and we'll talk to you later.