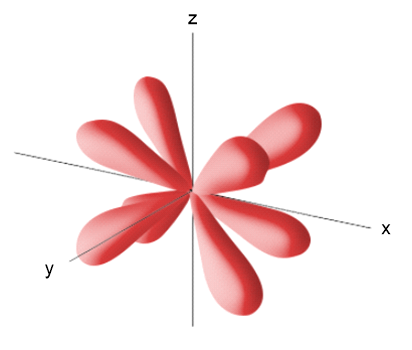
The contour representation of one of the orbitals for the n = 3 shell of a hydrogen atom is shown here. (a) What is the quantum number l for this orbital?
The accompanying drawing shows a contour plot for a dyz orbital. Consider the quantum numbers that could potentially correspond to this orbital. (c) What is the largest possible value of the magnetic quantum number, ml?
 Verified step by step guidance
Verified step by step guidance
Verified Solution
Key Concepts
Quantum Numbers

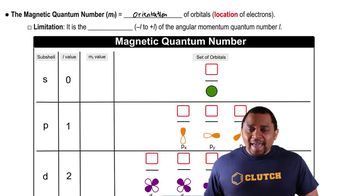
Magnetic Quantum Number (ml)
dyz Orbital

The contour representation of one of the orbitals for the n = 3 shell of a hydrogen atom is shown here. (c) In which of the following ways would you modify this sketch if the value of the magnetic quantum number, ml, were to change? (i) It would be drawn larger, (ii) the number of lobes would change, (iii) the lobes of the orbital would point in a different direction, (iv) there would be no change in the sketch.
The accompanying drawing shows a contour plot for a dyz orbital. Consider the quantum numbers that could potentially correspond to this orbital. (b) What is the value of the angular momentum quantum number, l?
The accompanying drawing shows a contour plot for a dyz orbital. Consider the quantum numbers that could potentially correspond to this orbital. (d) The probability density goes to zero along which of the following planes: xy, xz, or yz?
Four possible electron configurations for a carbon atom are shown below, but only one schematic represents the correct configuration for a carbon atom in its ground state. Which one is the correct electron configuration?
Four possible electron configurations for a nitrogen atom are shown below, but only one schematic represents the correct configuration for a nitrogen atom in its ground state. Which configurations violate the Pauli exclusion principle?
