Consider the unit cells shown here for three different structures that are commonly observed for metallic elements. (b) Which structure(s) corresponds to the least dense packing of atoms?
Calcium crystallizes in a body-centered cubic structure at 467°C. (a) How many Ca atoms are contained in each unit cell?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Body-Centered Cubic (BCC) Structure

Unit Cell
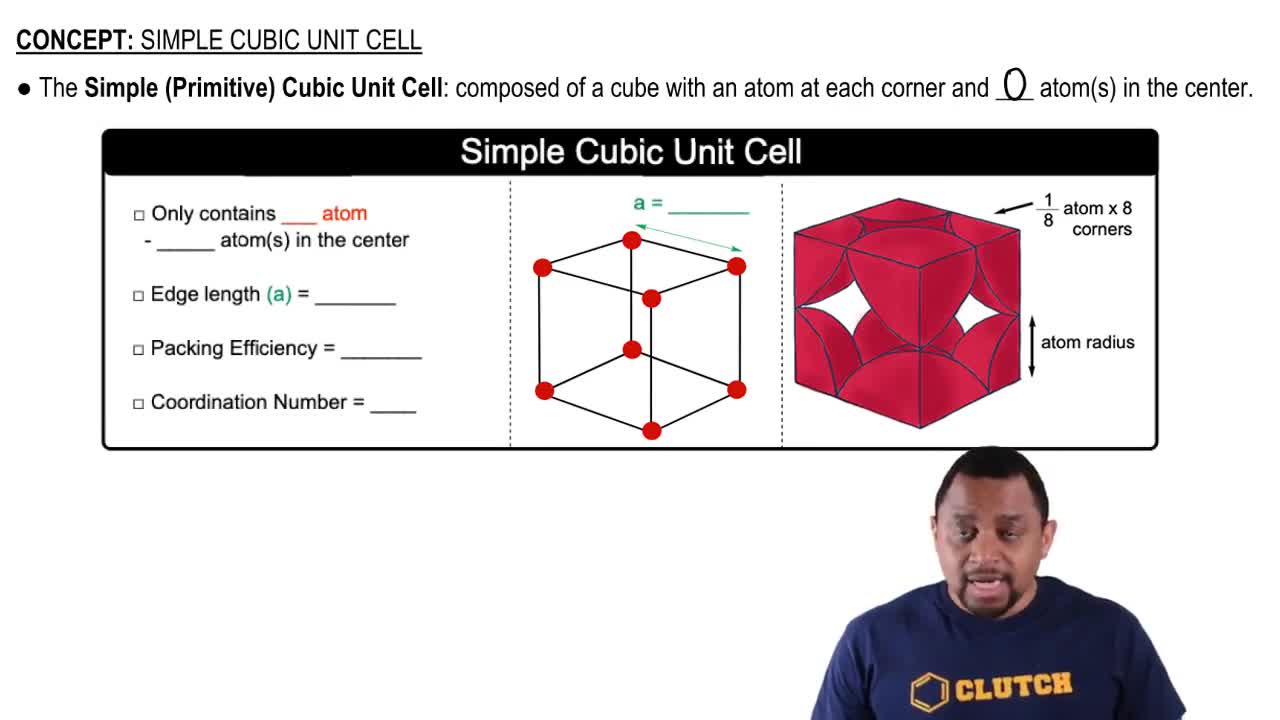
Atomic Packing Factor (APF)

Sodium metal (atomic weight 22.99 g/mol) adopts a body-centered cubic structure with a density of 0.97 g/cm3. (a) Use this information and Avogadro’s number (NA = 6.022 × 1023/mol) to estimate the atomic radius of sodium. (b) If sodium didn't react so vigorously, it could float on water. Use the answer from part (a) to estimate the density of Na if its structure were that of a cubic close-packed metal. Would it still float on water?
Calcium crystallizes in a body-centered cubic structure at 467°C. (b) How many nearest neighbors does each Ca atom possess? (c) Estimate the length of the unit cell edge, a, from the atomic radius of calcium (1.97 Å). (d) Estimate the density of Ca metal at this temperature.
Calcium crystallizes in a face-centered cubic unit cell at room temperature that has an edge length of 5.588 Å.
a. Calculate the atomic radius of a calcium atom.
b. Calculate the density of Ca metal at this temperature.
