Both Jacques Charles and Joseph Louis Guy-Lussac were avid balloonists. In his original flight in 1783, Jacques Charles used a balloon that contained approximately 31,150 L of H2. He generated the H2 using the reaction between iron and hydrochloric acid: Fe1s2 + 2 HCl1aq2 ¡ FeCl21aq2 + H21g2 How many kilograms of iron were needed to produce this volume of H2 if the temperature was 22 °C?
The atmospheric concentration of CO2 gas is presently 407 ppm (parts per million, by volume; that is, 407 L of every 106 L of the atmosphere are CO2). What is the mole fraction of CO2 in the atmosphere?.
 Verified step by step guidance
Verified step by step guidance
Verified Solution
Key Concepts
Mole Fraction
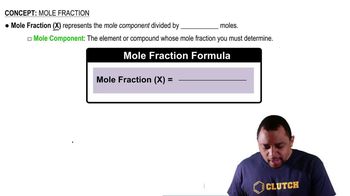
Parts Per Million (ppm)

Ideal Gas Law

Acetylene gas, C2H2(𝑔), can be prepared by the reaction of calcium carbide with water:
CaC2(𝑠)+2 H2O(𝑙)⟶Ca(OH)2(𝑎𝑞)+C2H2(𝑔)
Calculate the volume of C2H2 that is collected over water at 23°C by reaction of 1.524 g of CaC2 if the total pressure of the gas is 753 torr. (The vapor pressure of water is tabulated in Appendix B.)
Consider a mixture of two gases, A and B, confined in a closed vessel. A quantity of a third gas, C, is added to the same vessel at the same temperature. How does the addition of gas C affect the following: (a) the partial pressure of gas A?
A plasma-screen TV contains thousands of tiny cells filled with a mixture of Xe, Ne, and He gases that emits light of specific wavelengths when a voltage is applied. A particular plasma cell, 0.900 mm×0.300 mm×10.0 mm, contains Xe, Ne, and He atoms in a ratio of 1:12:12, respectively, at a total pressure of 500 torr at 298 K. Calculate the number of Xe, Ne, and He atoms in the cell.
A piece of dry ice (solid carbon dioxide) with a mass of 5.50 g is placed in a 10.0-L vessel that already contains air at 705 torr and 24°C. After the carbon dioxide has totally sublimed, what is the partial pressure of the resultant CO2 gas, and the total pressure in the container, at 24°C?
A sample of 5.00 mL of diethyl ether (C2H5OC2H5,density=0.7134 g/mL) is introduced into a 6.00-L vessel that already contains a mixture of N2 and O2, whose partial pressures are 𝑃N2=0.751atm and 𝑃O2=0.208atm. The temperature is held at 35.0°C, and the diethyl ether totally evaporates. b. Calculate the total pressure in the container.
