(a) A serving of a particular ready-to-serve brown & wild rice meal contains 4.5 g fat, 42 g carbohydrate, and 4.0 g protein. Estimate the number of calories in a serving.
The standard enthalpies of formation of gaseous propyne (C3H4), propylene (C3H6), and propane (C3H8) are +185.4, +20.4, and -103.8 kJ/mol, respectively. (b) Calculate the heat evolved on combustion of 1 kg of each substance.

Verified Solution
Key Concepts
Standard Enthalpy of Formation

Combustion Reaction
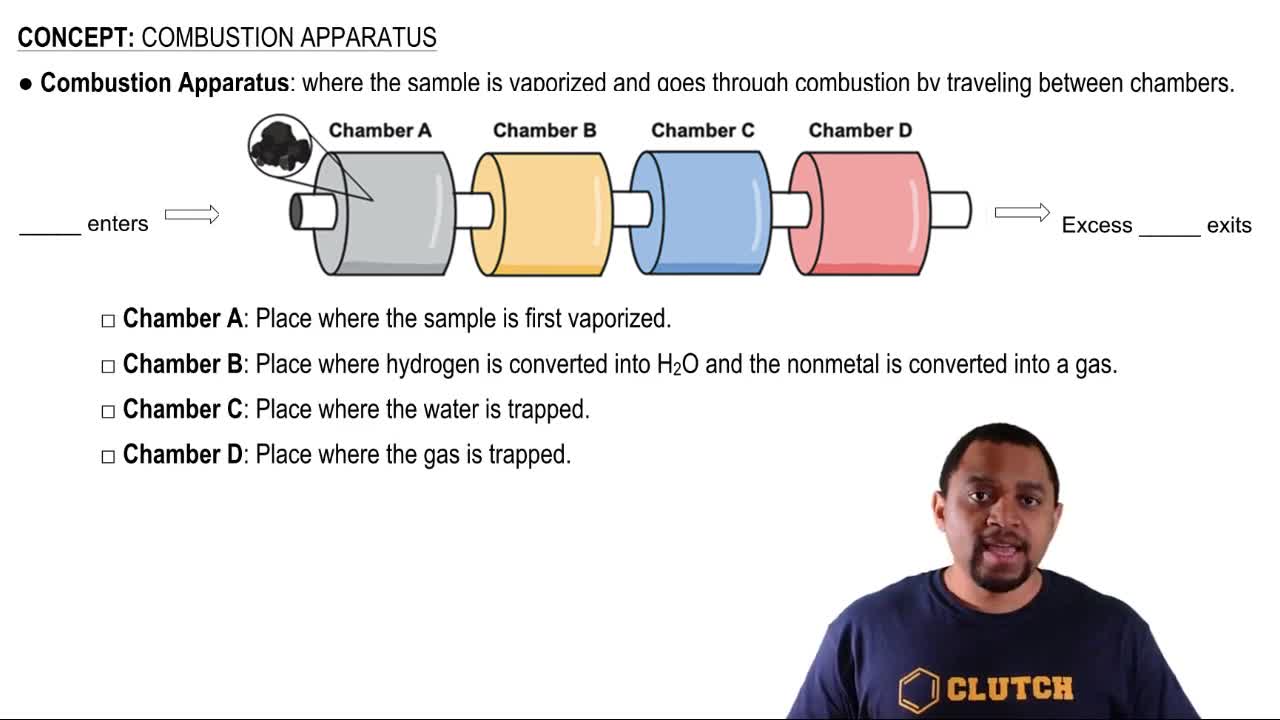
Heat of Combustion

The heat of combustion of fructose, C6H12O6, is -2812 kJ/mol. If a fresh golden delicious apple weighing 120 g contains 16.0 g of fructose, what caloric content does the fructose contribute to the apple?
The heat of combustion of ethanol, C2H5OH(l), is -1367 kJ/mol. A bottle of stout (dark beer) contains up to 6.0% ethanol by mass. Assuming the density of the beer to be 1.0 g/mL, what is the caloric content due to the alcohol (ethanol) in a bottle of beer (500 mL)?
The standard enthalpies of formation of gaseous propyne (C3H4), propylene (C3H6), and propane (C3H8) are +185.4, +20.4, and -103.8 kJ/mol, respectively. (c) Which is the most efficient fuel in terms of heat evolved per unit mass?
It is interesting to compare the 'fuel value' of a hydrocarbon in a hypothetical world where oxygen is not the combustion agent. The enthalpy of formation of CF4(g) is -679.9 kJ/mol. Which of the following two reactions is the more exothermic?
CH4(g) + 2 O2(g) → CO2(g) + 2 H2O(g)
CH4(g) + 4 F2(g) → CF4(g) + 4 HF(g)
At the end of 2012, global population was about 7.0 billion people. What mass of glucose in kg would be needed to provide 1500 Cal/person/day of nourishment to the global population for one year? Assume that glucose is metabolized entirely to CO2(𝑔) and H2O(𝑙) according to the following thermochemical equation: C6H12O6(s) + 6 O2(𝑔) → 6 CO2(𝑔) + 6 H2O(𝑙) ΔH° = -2803 kJ
