A 2.20-g sample of phenol (C₆H₅OH) was burned in a bomb calorimeter whose total heat capacity is 11.90 kJ/°C. The temperature of the calorimeter plus contents increased from 21.50 to 27.50 °C. (b) What is the heat of combustion per mole of phenol?

Verified step by step guidance

1. Calculate the temperature change (\( \Delta T \)) of the calorimeter by subtracting the initial temperature from the final temperature: \( \Delta T = T_{\text{final}} - T_{\text{initial}} \).
2. Use the formula for heat absorbed by the calorimeter: \( q = C_{\text{cal}} \times \Delta T \), where \( C_{\text{cal}} \) is the heat capacity of the calorimeter.
3. Determine the moles of phenol burned using its molar mass: \( \text{moles of phenol} = \frac{\text{mass of phenol}}{\text{molar mass of phenol}} \).
4. Calculate the heat of combustion per mole of phenol by dividing the total heat absorbed by the calorimeter by the moles of phenol: \( \Delta H_{\text{combustion}} = \frac{q}{\text{moles of phenol}} \).
5. Ensure the sign of \( \Delta H_{\text{combustion}} \) is negative, as combustion is an exothermic process.

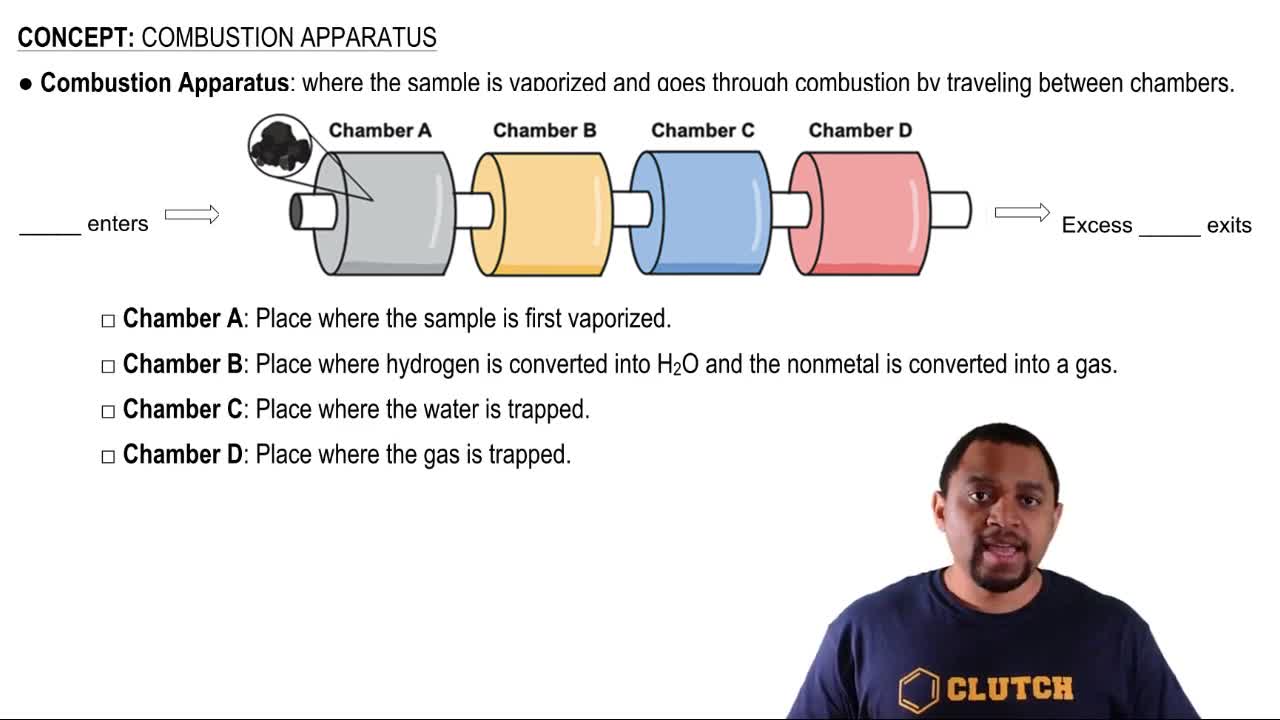
Key Concepts

Heat Capacity

Heat capacity is the amount of heat required to change the temperature of a substance by one degree Celsius. In calorimetry, the heat capacity of the calorimeter is crucial for determining the total heat absorbed or released during a reaction. It is calculated by multiplying the heat capacity by the change in temperature, allowing us to quantify the energy changes involved in the combustion process.

Molar Mass

Molar mass is the mass of one mole of a substance, typically expressed in grams per mole (g/mol). For phenol (C6H5OH), the molar mass can be calculated by summing the atomic masses of its constituent elements. Knowing the molar mass is essential for converting the mass of phenol burned into moles, which is necessary for calculating the heat of combustion per mole.

Heat of Combustion

The heat of combustion is the amount of energy released when one mole of a substance is completely burned in oxygen. It is typically expressed in kilojoules per mole (kJ/mol). To find the heat of combustion for phenol, the total heat released during the combustion process, calculated from the calorimeter's temperature change, is divided by the number of moles of phenol burned, providing a measure of the energy content of the fuel.