The accompanying graph illustrates the decay of 88 42 Mo, which decays via positron emission. (d) What is the product of the decay process? [Section 21.4]

Hello. Everyone in this video. The following graph right over here shows the decay of this by positron emission. In this question, we're being told to identify the nuclear I'd produced in this radioactive decay. So for a positron, we have zero plus one and E. And what does zero represents here? This is going to be where the mass number goes. This right here on the bottom is our atomic number. And for the product. So this is positron. And then for the product it can be represented as a Z. And X. So this A here is going to be the mass number for atomic number. That's going to be easy. And X is going to be the element symbol. So for my reaction we have course the 86 R. N. That goes to a Z. X. And zero plus one and E. So for the mass number of reactions this equals to the mass number of products. So we have let's do this in a different color. So 211 equals two A plus zero. Which then just means that A. Is equal to +211. And for the atomic number of reactors this equals the atomic number of products. So for this we have again, different color. Let's see we have 86 equaling two Z plus one. So we just subtract one to isolate the Z. So 86 minus one equals to Z. Of course that is just 85. So again the atomic number being at 85 here, we spoke at the period table. And this gives us um a team. Let's spread this in right at the bottom. So we see atomic number of Z Is equal to 85 and this is going to be 80. Alright, so then our students in different color, the new Clyde that is being produced is going to be then 85. A. T. Again, right over here, this is going to be our mass number 85 is our atomic number and element symbol of A. T. So my final answer is going to be this right over here.

Ch.21 - Nuclear Chemistry

All textbooks

Brown 14th Edition

Ch.21 - Nuclear Chemistry

Problem 6d

Chapter 21, Problem 6d

The accompanying graph illustrates the decay of ⁸⁸₄₂Mo, which decays via positron emission. (d) What is the product of the decay process? [Section 21.4]

Verified step by step guidance

Identify the initial isotope undergoing decay: ^{88}_{42}Mo.

Determine the type of decay: positron emission (β^+ decay).

Write the nuclear equation for positron emission: ^{88}_{42}Mo → ^{88}_{41}Nb + β^+.

Identify the product of the decay process: the new element formed is Niobium (Nb) with a mass number of 88 and an atomic number of 41.

Verify the conservation of mass and atomic numbers in the nuclear equation to ensure the correctness of the product.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Radioactive Decay

Radioactive decay is the process by which an unstable atomic nucleus loses energy by emitting radiation. This can occur through various modes, including alpha decay, beta decay, and positron emission. In the case of positron emission, a proton in the nucleus is transformed into a neutron, releasing a positron and a neutrino, which results in a decrease in the atomic number of the element.

Decay Products

The decay product is the new element or isotope formed as a result of radioactive decay. For example, when molybdenum-88 ( 88 42Mo) undergoes positron emission, it transforms into a different element with a lower atomic number. Understanding the decay products is crucial for applications in nuclear chemistry, medicine, and radiometric dating.

Half-Life

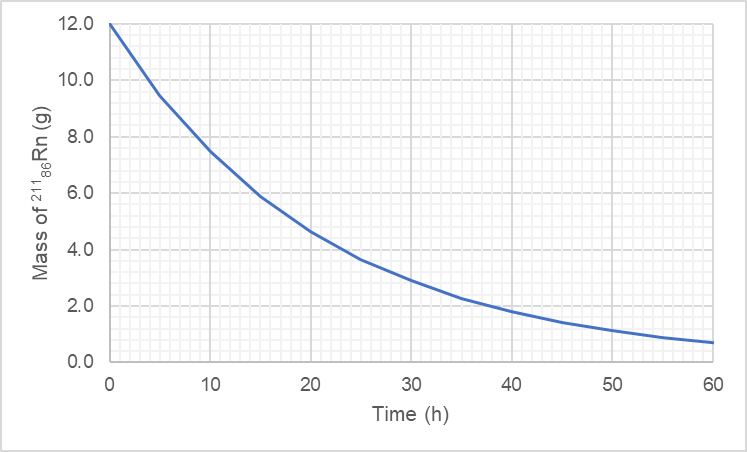
Half-life is the time required for half of the radioactive nuclei in a sample to decay. This concept is essential for predicting the behavior of radioactive substances over time. The graph provided illustrates the decay of radon-218, showing how the mass decreases exponentially, which is characteristic of half-life behavior in radioactive decay processes.

Recommended video:

Guided course

02:17

Zero-Order Half-life

Related Practice

Textbook Question

The accompanying graph illustrates the decay of ⁸⁸₄₂Mo, which decays via positron emission. (a) What is the halflife of the decay? [Section 21.4]

580

views

Textbook Question

The accompanying graph illustrates the decay of ⁸⁸₄₂Mo, which decays via positron emission. (b) What is the rate constant for the decay? [Section 21.4]

350

views

Textbook Question

The accompanying graph illustrates the decay of ⁸⁸₄₂Mo, which decays via positron emission. (c) What fraction of the original sample of ⁸⁸₄₂Mo remains after 12 min? [Section 21.4]

495

views

Open Question

A 65-kg person is accidentally exposed for 240 s to a 15-mCi source of beta radiation coming from a sample of 90Sr. (a) What is the activity of the radiation source in disintegrations per second? In becquerels? (b) Each beta particle has an energy of 8.75 * 10^-14 J, and 7.5% of the radiation is absorbed by the person. Assuming that the absorbed radiation is spread over the person’s entire body, calculate the absorbed dose in rads and in grays. (c) If the RBE of the beta particles is 1.0, what is the effective dose in mrem and in sieverts? (d) Is the radiation dose equal to, greater than, or less than that for a typical mammogram (300 mrem)?

Textbook Question

All the stable isotopes of boron, carbon, nitrogen, oxygen, and fluorine are shown in the accompanying chart (in red), along with their radioactive isotopes with t1>2 7 1 min (in blue). (b) Which radioactive isotopes are most likely to decay by beta emission? [Sections 21.2, 21.4, and 21.5]

844

views

Open Question

A sample of an alpha emitter having an activity of 0.18 Ci is stored in a 25.0-mL sealed container at 22 _x001D_C for 245 days. (b) Assuming that each alpha particle is converted to a helium atom, what is the partial pressure of helium gas in the container after this 245-day period?

The accompanying graph illustrates the decay of 8842Mo, which decays via positron emission. (d) What is the product of the decay process? [Section 21.4]

Verified video answer for a similar problem:

Key Concepts

Radioactive Decay

Decay Products

Half-Life

The accompanying graph illustrates the decay of ⁸⁸₄₂Mo, which decays via positron emission. (d) What is the product of the decay process? [Section 21.4]