The kinetic energy of a rolling billiard ball is given by KE = 1/2 mv2. Suppose a 0.17-kg billiard ball is rolling down a pool table with an initial speed of 4.5 m/s. As it travels, it loses some of its energy as heat. The ball slows down to 3.8 m/s and then collides head-on with a second billiard ball of equal mass. The first billiard ball completely stops and the second one rolls away with a velocity of 3.8 m/s. Assume the first billiard ball is the system. Calculate q.
LP gas burns according to the exothermic reaction: C3H8(g) + 5 O2(g) → 3 CO2(g) + 4 H2O(g) ΔH°rxn = –2044 kJ What mass of LP gas is necessary to heat 1.5 L of water from room temperature (25.0 °C) to boiling (100.0 °C)? Assume that during heating, 15% of the heat emitted by the LP gas combustion goes to heat the water. The rest is lost as heat to the surroundings.
 Verified step by step guidance
Verified step by step guidance
Verified Solution
Key Concepts
Exothermic Reactions
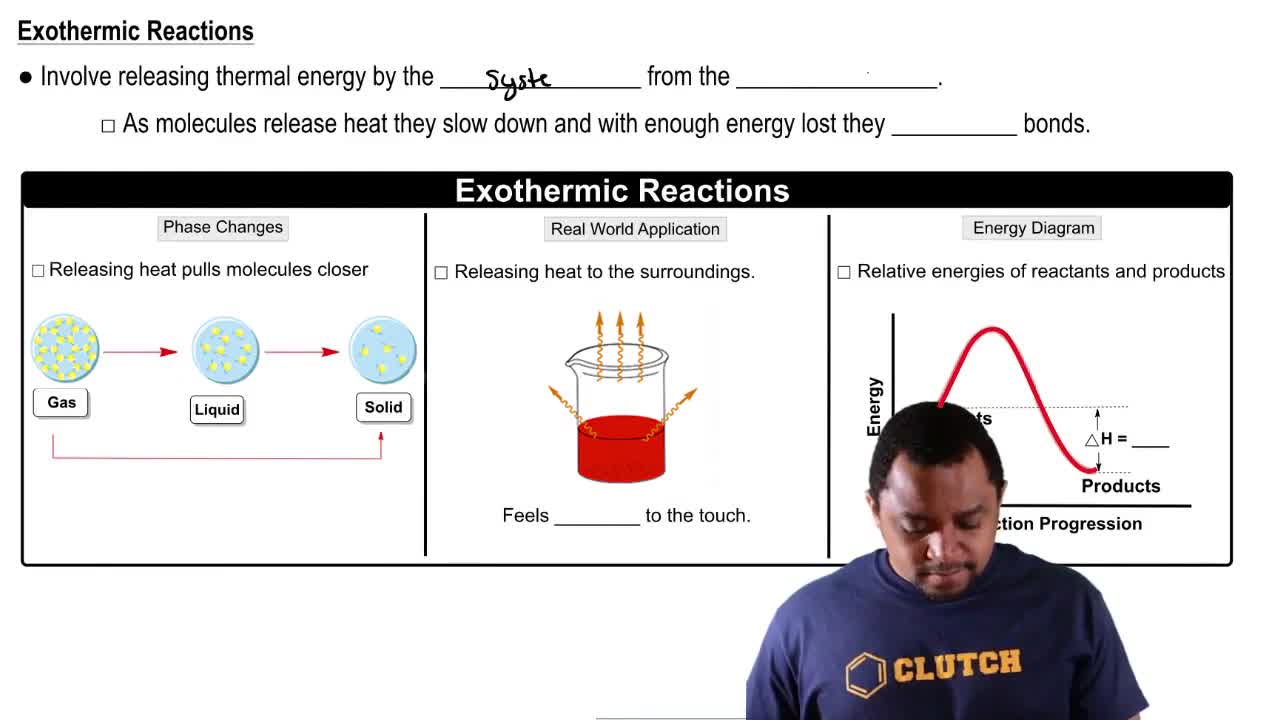
Heat Transfer and Specific Heat Capacity

Energy Efficiency in Heating

Use standard enthalpies of formation to calculate the standard change in enthalpy for the melting of ice. (The ΔH°f for H2O(s) is –291.8 kJ/mol.)
Use standard enthalpies of formation to calculate the standard change in enthalpy for the melting of ice. (The ΔH°f for H2O(s) is –291.8 kJ/mol.) Use this value to calculate the mass of ice required to cool 355 mL of a beverage from room temperature (25.0 °C) to 0.0 °C. Assume that the specific heat capacity and density of the beverage are the same as those of water.
Dry ice is solid carbon dioxide. Instead of melting, solid carbon dioxide sublimes according to the equation: CO2(s) → CO2(g) ◀ When carbon dioxide sublimes, the gaseous CO2 is cold enough to cause water vapor in the air to condense, forming fog. When dry ice is added to warm water, heat from the water causes the dry ice to sublime more quickly. The evaporating carbon dioxide produces a dense fog often used to create special effects. In a simple dry ice fog machine, dry ice is added to warm water in a Styrofoam cooler. The dry ice produces fog until it evaporates away, or until the water gets too cold to sublime the dry ice quickly enough. Suppose that a small Styrofoam cooler holds 15.0 L of water heated to 85 °C. Use standard enthalpies of formation to calculate the change in enthalpy for dry ice sublimation, and calculate the mass of dry ice that should be added to the water so that the dry ice completely sublimes away when the water reaches 25 °C. Assume no heat loss to the surroundings. (The ΔH°f for CO2(s) is –427.4 kJ/mol.)
