Here are the essential concepts you must grasp in order to answer the question correctly.
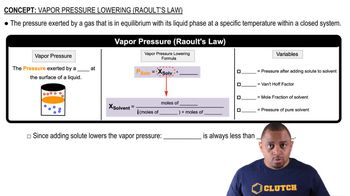
Vapor Pressure
Vapor pressure is the pressure exerted by a vapor in equilibrium with its liquid or solid phase at a given temperature. It reflects the tendency of particles to escape from the liquid phase into the vapor phase. A higher vapor pressure indicates a greater volatility of the substance, which is crucial for understanding phase changes and calculating thermodynamic properties like enthalpy of vaporization.
Recommended video:
Raoult's Law and Vapor Pressure
Enthalpy of Vaporization (ΔH<sub>vap</sub>)
The enthalpy of vaporization (ΔH<sub>vap</sub>) is the amount of energy required to convert a unit quantity of a liquid into vapor at constant temperature and pressure. It is a critical parameter in thermodynamics that helps quantify the energy changes associated with phase transitions. This value can be determined using the Clausius-Clapeyron equation, which relates vapor pressure and temperature to ΔH<sub>vap</sub>.
Recommended video:
Enthalpy of Vaporization Example
Clausius-Clapeyron Equation
The Clausius-Clapeyron equation describes the relationship between the vapor pressure of a substance and its temperature, allowing for the calculation of the enthalpy of vaporization. It is expressed as d(ln P)/dT = ΔH<sub>vap</sub>/(RT²), where P is the vapor pressure, T is the temperature, R is the ideal gas constant, and ΔH<sub>vap</sub> is the enthalpy of vaporization. This equation is essential for solving problems involving phase changes and thermodynamic properties.
Recommended video:
Clausius-Clapeyron Equation