Here are the essential concepts you must grasp in order to answer the question correctly.
Linear Equations
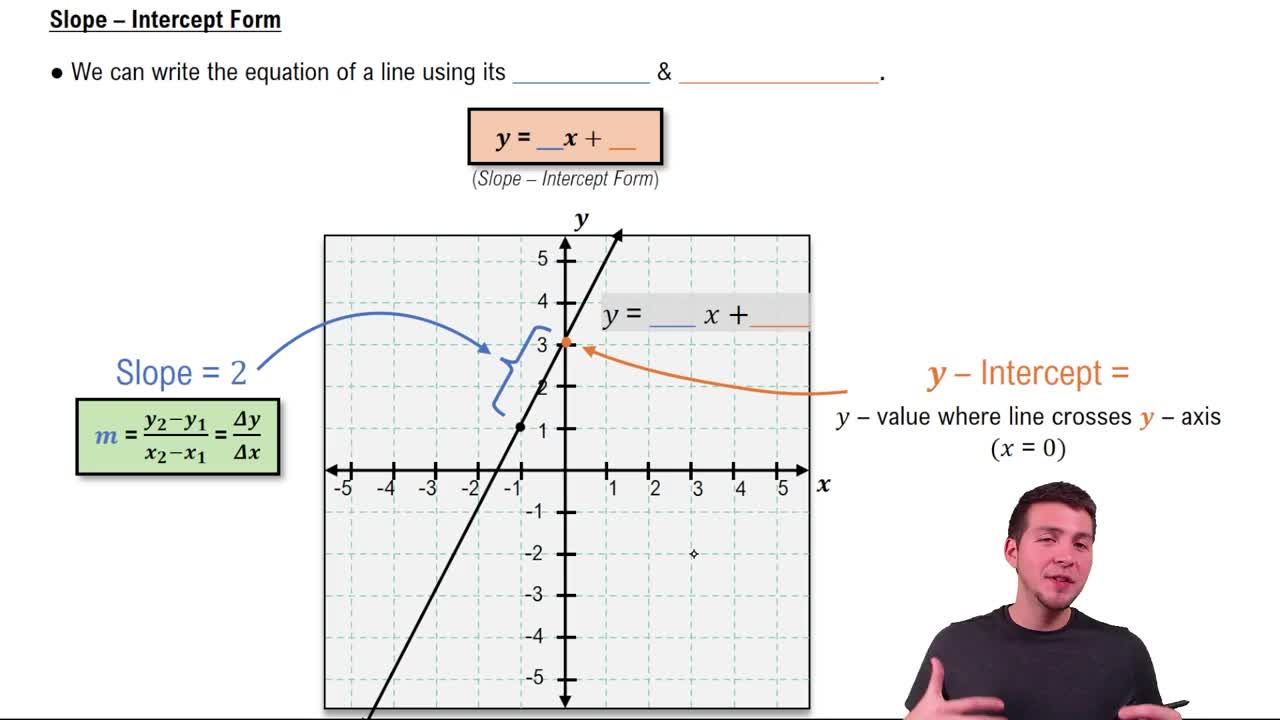
A linear equation is an algebraic expression that represents a straight line when graphed on a coordinate plane. It typically takes the form y = mx + b, where m is the slope and b is the y-intercept. Understanding linear equations is essential for graphing, as it allows students to identify how changes in x affect y.
Recommended video:
Categorizing Linear Equations
Slope-Intercept Form
The slope-intercept form of a linear equation is expressed as y = mx + b, where m represents the slope of the line and b represents the y-intercept. The slope indicates the steepness and direction of the line, while the y-intercept is the point where the line crosses the y-axis. This form is particularly useful for quickly identifying key characteristics of the graph.
Recommended video:
Graphing Points
Graphing points involves plotting specific (x, y) coordinates on a Cartesian plane. For the given equation, substituting values of x allows us to calculate corresponding y values, creating a set of points that can be plotted. Understanding how to graph points is crucial for visualizing the relationship defined by the equation and for accurately drawing the line.
Recommended video:
Graphing Equations of Two Variables by Plotting Points
 Verified step by step guidance
Verified step by step guidance