Quadratic functions are a specific type of polynomial function characterized by their degree of 2. The standard form of a quadratic function is expressed as \( f(x) = ax^2 + bx + c \), where \( a \), \( b \), and \( c \) are real numbers, and \( a \) cannot be zero. The graph of any quadratic function takes the shape of a parabola, which can open either upward or downward depending on the sign of \( a \).
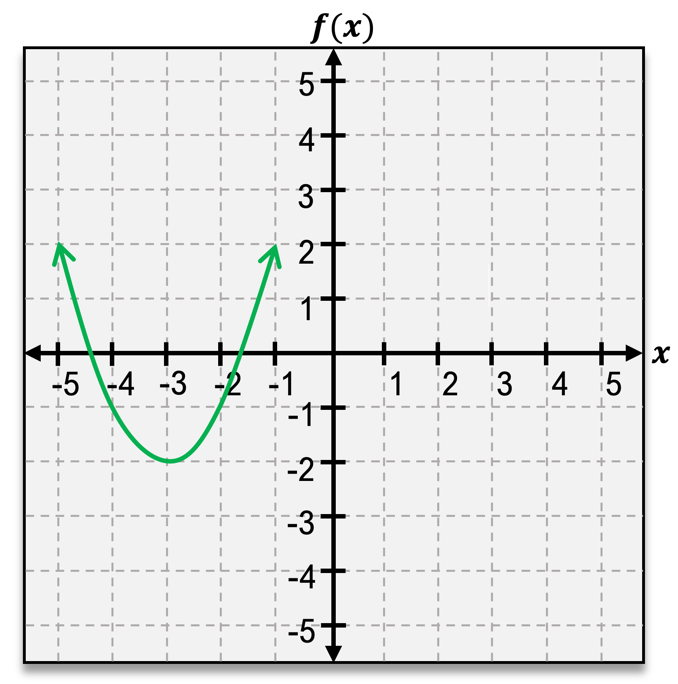
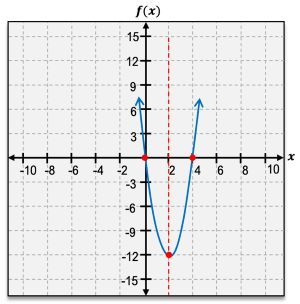
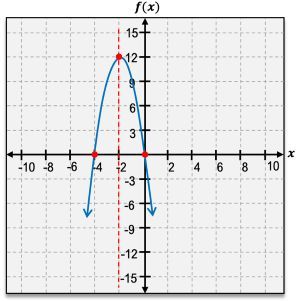
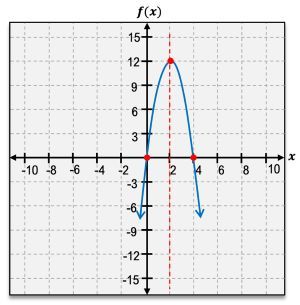
The vertex of a parabola is a crucial feature, representing either the highest or lowest point on the graph. If the parabola opens upward, the vertex is a minimum point; if it opens downward, the vertex is a maximum point. The vertex is denoted as an ordered pair, such as \( (h, k) \), where \( h \) and \( k \) are the x and y coordinates, respectively.
Another important aspect of quadratic functions is the x-intercepts, which are the points where the graph crosses the x-axis. A quadratic function can have either one or two x-intercepts, but never more or less. The y-intercept, on the other hand, is where the graph intersects the y-axis, and it can be found by evaluating \( f(0) \).
The axis of symmetry is a vertical line that divides the parabola into two mirror-image halves, always passing through the vertex. It can be expressed as \( x = h \), where \( h \) is the x-coordinate of the vertex.
When analyzing the domain and range of quadratic functions, the domain is always all real numbers, represented as \( (-\infty, \infty) \). The range, however, depends on whether the vertex is a minimum or maximum. For a minimum point, the range extends from the vertex's y-coordinate to infinity, while for a maximum point, it extends from negative infinity to the vertex's y-coordinate.
Additionally, understanding the intervals of increase and decrease is essential. A parabola increases on the interval from negative infinity to the vertex and decreases from the vertex to positive infinity. This behavior is determined by the vertex's position, which acts as a dividing point for these intervals.
Quadratic functions can also be expressed in vertex form, which is particularly useful for graphing. The vertex form is given by \( f(x) = a(x - h)^2 + k \), where \( (h, k) \) is the vertex of the parabola. This form allows for easier identification of the vertex and the direction in which the parabola opens.