Here are the essential concepts you must grasp in order to answer the question correctly.
Transformations of Functions
Transformations of functions involve altering the graph of a parent function through shifts, stretches, compressions, and reflections. For example, vertical shifts move the graph up or down, while horizontal shifts move it left or right. Understanding these transformations is crucial for describing how the graph of a function changes from its original form.
Recommended video:
Domain & Range of Transformed Functions
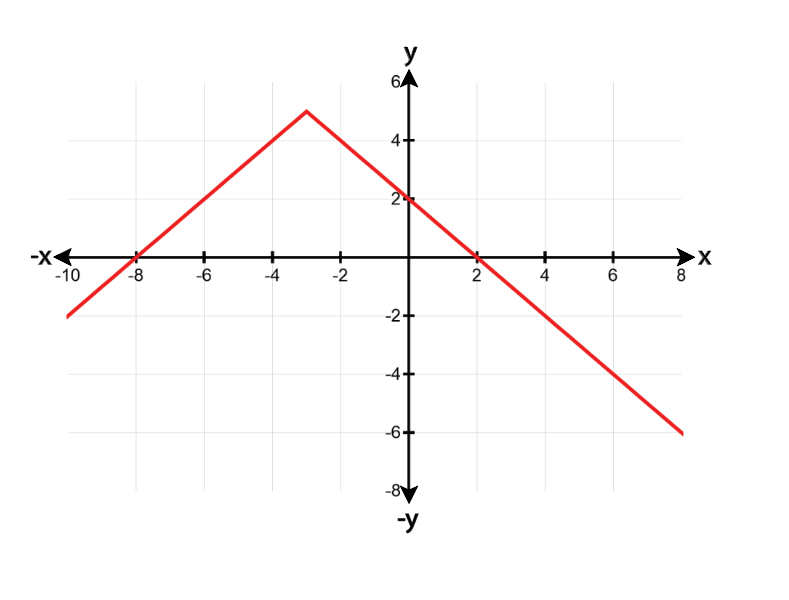
Absolute Value Function
The absolute value function, denoted as f(x) = |x|, produces a V-shaped graph that reflects all negative values of x to positive values. This function is essential in understanding how transformations affect its shape and position. When transformed, the peaks and slopes of the graph can change, indicating shifts or reflections.
Recommended video:
Square Root Function
The square root function, represented as g(x) = √x, produces a graph that starts at the origin and increases gradually. This function is important for understanding transformations that may involve vertical or horizontal shifts, as well as reflections. Analyzing how this function behaves under transformations helps in predicting the resulting graph's characteristics.
Recommended video:
Imaginary Roots with the Square Root Property
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 5:25m
5:25m