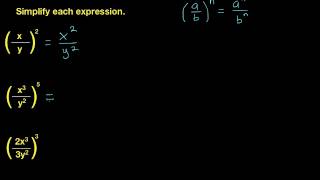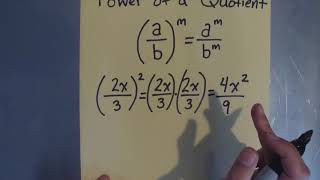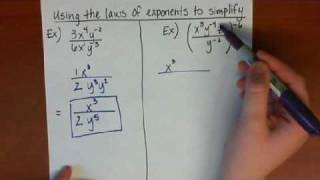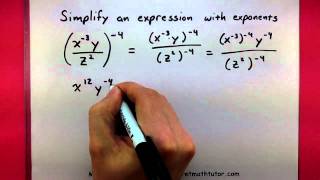Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Exponents
Problem 53c
Textbook Question
Textbook QuestionIn Exercises 51–58, solve each equation. Express the solution in scientific notation. x / 2X10⁸ =-3.1X10⁻⁵
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Scientific Notation
Scientific notation is a way of expressing numbers that are too large or too small in a compact form. It is written as a product of a number between 1 and 10 and a power of ten. For example, 3.1 x 10⁻⁵ represents 0.000031. Understanding how to convert between standard form and scientific notation is essential for solving equations involving such numbers.
Recommended video:

Interval Notation
Solving Linear Equations
A linear equation is an equation of the first degree, meaning it involves only linear terms. To solve a linear equation, one typically isolates the variable on one side of the equation. In the given problem, manipulating the equation to isolate 'x' involves basic algebraic operations such as multiplication and division.
Recommended video:

Solving Linear Equations with Fractions
Properties of Equality
The properties of equality state that if two expressions are equal, then performing the same operation on both sides will maintain the equality. This includes addition, subtraction, multiplication, and division. Applying these properties is crucial when rearranging equations to solve for the unknown variable, ensuring that the solution remains valid.
Recommended video:

Change of Base Property

 7:39m
7:39mWatch next
Master Introduction to Exponent Rules with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice