Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Intro to Functions & Their Graphs
Problem 111
Textbook Question
In Exercises 109–111, give the center and radius of each circle. x^2 + y^2 - 4x + 2y - 4 = 0
 Verified step by step guidance
Verified step by step guidance1
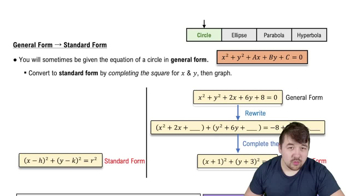
Rewrite the equation in the form of a circle equation: \((x - h)^2 + (y - k)^2 = r^2\).
Group the \(x\) terms and \(y\) terms together: \(x^2 - 4x + y^2 + 2y = 4\).
Complete the square for the \(x\) terms: \(x^2 - 4x\).
Complete the square for the \(y\) terms: \(y^2 + 2y\).
Rewrite the equation with completed squares to identify the center \((h, k)\) and radius \(r\).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Standard Form of a Circle
The standard form of a circle's equation is (x - h)² + (y - k)² = r², where (h, k) is the center and r is the radius. This form allows for easy identification of the circle's center and radius by comparing it to the general equation of a circle.
Recommended video:

Circles in Standard Form
Completing the Square
Completing the square is a method used to transform a quadratic equation into a perfect square trinomial. This technique is essential for rewriting the given circle equation in standard form, enabling the identification of the center and radius.
Recommended video:

Solving Quadratic Equations by Completing the Square
Quadratic Terms in Circle Equations
In circle equations, the quadratic terms x² and y² represent the dimensions of the circle in the Cartesian plane. Understanding how these terms interact with linear terms (like -4x and +2y) is crucial for manipulating the equation to find the circle's center and radius.
Recommended video:
Circles in General Form

 5:2m
5:2mWatch next
Master Relations and Functions with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice






