Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
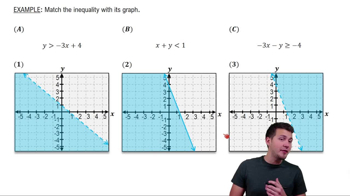
Graphing Systems of Inequalities
Problem 65a
Textbook Question
Graph the solution set of each system of inequalities.
y≤logx
y≥∣x−2∣
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the inequalities. The first inequality y \leq \log x represents the region below or on the curve of the logarithmic function y = \log x. The second inequality y \geq |x - 2| represents the region above or on the V-shaped graph of the absolute value function y = |x - 2|.
Step 2: Graph the first inequality y \leq \log x. Start by plotting the curve y = \log x, which is defined for x > 0. This curve passes through the point (1, 0) and increases slowly as x increases. Shade the region below this curve, including the curve itself, to represent y \leq \log x.
Step 3: Graph the second inequality y \geq |x - 2|. The graph of y = |x - 2| is a V-shaped graph with its vertex at (2, 0). The left arm of the V has a slope of -1, and the right arm has a slope of 1. Shade the region above this V-shaped graph, including the graph itself, to represent y \geq |x - 2|.
Step 4: Identify the solution set. The solution set of the system of inequalities is the region where the shaded areas from both inequalities overlap. This is the area that satisfies both y \leq \log x and y \geq |x - 2|.
Step 5: Verify the solution set. Check a few points within the overlapping region to ensure they satisfy both inequalities. For example, choose a point like (3, 0.5) and verify that it satisfies both y \leq \log x and y \geq |x - 2|.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
10mPlay a video:
Was this helpful?

 7:2m
7:2mWatch next
Master Linear Inequalities with a bite sized video explanation from Patrick Ford
Start learning