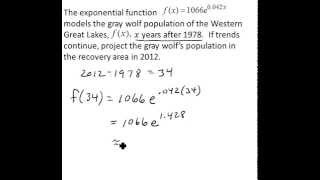Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
6. Exponential & Logarithmic Functions
The Number e
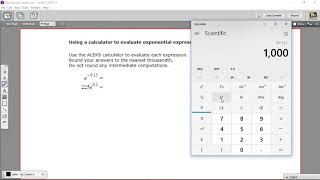
Problem 63
Textbook Question
Textbook QuestionIn Exercises 61–64, give the equation of each exponential function whose graph is shown. 
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Exponential Functions
Exponential functions are mathematical expressions of the form f(x) = a * b^x, where 'a' is a constant, 'b' is the base (a positive real number), and 'x' is the exponent. These functions are characterized by their rapid growth or decay, depending on the value of 'b'. Understanding the general shape and behavior of exponential functions is crucial for analyzing their graphs.
Recommended video:

Exponential Functions
Graphing Exponential Functions
Graphing exponential functions involves plotting points based on the function's equation and understanding key features such as intercepts, asymptotes, and the direction of growth or decay. The graph typically approaches a horizontal asymptote, which is often the x-axis, and can cross the y-axis at the point (0, a). Identifying these features helps in accurately representing the function visually.
Recommended video:

Graphs of Exponential Functions
Finding the Equation from Points
To find the equation of an exponential function from given points on its graph, one can use the coordinates of these points to set up a system of equations. By substituting the x-values into the general form of the exponential function, you can solve for the constants 'a' and 'b'. This process often involves logarithmic calculations to isolate the base and determine the function's specific characteristics.
Recommended video:
Guided course

Finding Equations of Lines Given Two Points
Related Videos
Related Practice