Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
Graphing Systems of Inequalities
Problem 66
Textbook Question
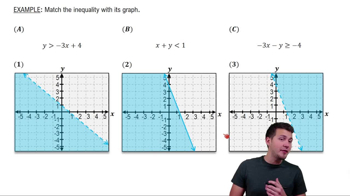
Graph the solution set of each system of inequalities.
ex−y≤1
x−2y≥4
 Verified step by step guidance
Verified step by step guidance1
Step 1: Start by graphing the first inequality, \( e^x - y \leq 1 \). To do this, first graph the boundary line \( y = e^x - 1 \). This is an exponential function shifted down by 1 unit. Plot several points for \( x \) values and connect them to form the curve.
Step 2: Determine which side of the boundary line \( y = e^x - 1 \) to shade. Choose a test point not on the line, such as (0,0). Substitute into the inequality: \( e^0 - 0 \leq 1 \) simplifies to \( 1 \leq 1 \), which is true. Therefore, shade the region below the curve.
Step 3: Next, graph the second inequality, \( x - 2y \geq 4 \). Start by graphing the boundary line \( x - 2y = 4 \). Rearrange to slope-intercept form: \( y = \frac{x}{2} - 2 \). Plot the y-intercept at (0, -2) and use the slope \( \frac{1}{2} \) to find another point.
Step 4: Determine which side of the line \( y = \frac{x}{2} - 2 \) to shade. Use the test point (0,0) again: \( 0 - 2(0) \geq 4 \) simplifies to \( 0 \geq 4 \), which is false. Therefore, shade the region above the line.
Step 5: The solution set of the system of inequalities is the region where the shaded areas from both inequalities overlap. Identify this region on the graph, ensuring to use dashed or solid lines appropriately based on whether the inequalities are strict or inclusive.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
9mPlay a video:
Was this helpful?

 7:2m
7:2mWatch next
Master Linear Inequalities with a bite sized video explanation from Patrick Ford
Start learning