0. Functions
Introduction to Functions
Practice this topic
- Multiple Choice
State the inputs and outputs of the following relation. Is it a function?
1187views31rank - Multiple Choice
State the inputs and outputs of the following relation. Is it a function? {}
878views27rank - Multiple Choice
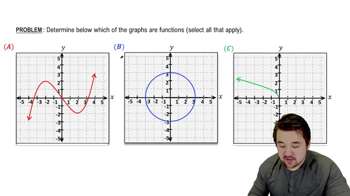
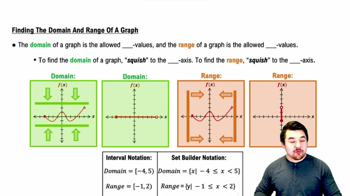
Find the domain and range of the following graph (write your answer using interval notation).
913views23rank - Textbook Question
Decide whether , , or both represent one-to-one functions. <IMAGE>
412views1rank - Textbook Question
Daylight function for 40 °N Verify that the function has the following properties, where t is measured in days and D is the number of hours between sunrise and sunset. It has a period of 365 days.
393views - Textbook Question
Daylight function for 40 °N Verify that the function has the following properties, where t is measured in days and D is the number of hours between sunrise and sunset.
Its maximum and minimum values are 14.8 and 9.2, respectively, which occur approximately at and , respectively (corresponding to the solstices).
433views - Textbook Question
Daylight function for 40 °N Verify that the function has the following properties, where t is measured in days and D is the number of hours between sunrise and sunset.
and (corresponding to the equinoxes).
422views - Multiple Choice
If , what is the value of ?
76views