Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
0. Functions
Inverse Trigonometric Functions
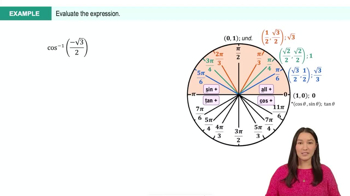
Problem 89
Textbook Question
Express θ in terms of x using the inverse sine, inverse tangent, and inverse secant functions. <IMAGE>
 Verified step by step guidance
Verified step by step guidance1
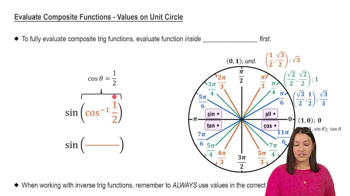
Identify the trigonometric relationships given in the problem. Typically, this involves recognizing the sides of a right triangle or the coordinates of a point on the unit circle.
Express the angle \( \theta \) in terms of \( x \) using the inverse sine function. Recall that \( \theta = \sin^{-1}(x) \) when \( x \) is the opposite side over the hypotenuse in a right triangle.
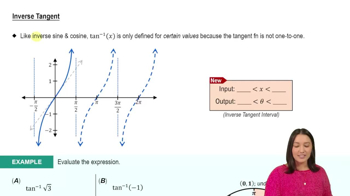
Express the angle \( \theta \) in terms of \( x \) using the inverse tangent function. Remember that \( \theta = \tan^{-1}(x) \) when \( x \) is the opposite side over the adjacent side in a right triangle.
Express the angle \( \theta \) in terms of \( x \) using the inverse secant function. Note that \( \theta = \sec^{-1}(x) \) when \( x \) is the hypotenuse over the adjacent side in a right triangle.
Combine these expressions to find a consistent expression for \( \theta \) in terms of \( x \) using the given inverse trigonometric functions. Ensure that the domain and range of each function are considered to maintain validity.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
Was this helpful?
Related Videos
Related Practice