Identify the most helpful first step in verifying the identity. ( tan ⁡ 2 θ sin ⁡ 2 θ − 1 ) = sec ⁡ 2 θ sin ⁡ 2 ( − θ ) \left(\frac{\tan^2\theta}{\sin^2\theta}-1\right)=\sec^2\theta\sin^2\left(-\theta\right) ( s i n 2 θ t a n 2 θ − 1 ) = sec 2 θ sin 2 ( − θ )

In this problem, we're asked to identify the most helpful first step in verifying the identity. Now just because it's the most helpful first step does not mean that it's the only first step that you could take. So if you have a different idea for what step you could have taken first in verifying this identity, that's totally okay. I'm just gonna show you here what would be the most helpful in getting started verifying this identity and being able to do it in the least amount of steps. So let's go ahead and get started here. Now looking at this equation, I have the tangent squared of theta over the sine squared of theta minus minus 1, and this is equal to the secant squared of theta times the sine squared of negative theta. Now what should we do first? Well remember that when working with equations that have two sides that we need to simplify, we want to start with a more complicated side first. Now to me looking at this equation, my left side is more complicated because it not only has squared trig functions, but it has a fraction. So this is a more complicated side. So we need to start by doing something to this left side, but what should we do? Well, looking at this, I have a tangent squared over a sine squared, and I can rewrite tangent in terms of sine and cosine. So that would be the most helpful first step here because it will lead us to be able to cancel things out. Now let's go ahead and see what happens when I take that step. Now rewriting that tangent squared in terms of sine and cosine gives me the sine squared of theta over the cosine squared of theta, and that is all over that denominator sine squared of theta. Now I still have that minus 1 and that's what's on my left side there. Now looking at this, I'm able to cancel sine squared, and I'm left with a much more simple fraction, 1 over the cosine squared of theta minus 1. Now from here, I would continue to verify this identity. So here our most helpful first step would actually be rewriting that tangent squared of theta on that left side. Thanks for watching and I'll see you in the next one.

0. Functions

Trigonometric Identities

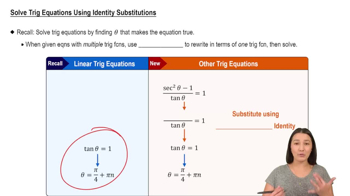
Calculus0. FunctionsTrigonometric Identities

Multiple Choice

Identify the most helpful first step in verifying the identity.
$\left(\frac{\tan^2\theta}{\sin^2\theta}-1\right)=\sec^2\theta\sin^2\left(-\theta\right)$

Add the terms on the left side using a common denominator.

Rewrite left side of equation in terms of sine and cosine.

Use even-odd identity to eliminate negative argument on right side of equation.

Rewrite right side of equation in terms of sine and cosine.

views

My Courses

Chemistry

Biology

Math

Physics

Business

Social Sciences

Programming

Product & Marketing

Identify the most helpful first step in verifying the identity.
$\left(\frac{\tan^2\theta}{\sin^2\theta}-1\right)=\sec^2\theta\sin^2\left(-\theta\right)$

My Courses

Chemistry

Biology

Math

Physics

Business

Social Sciences

Programming

Product & Marketing

Identify the most helpful first step in verifying the identity.﻿(tan⁡2θsin⁡2θ−1)=sec⁡2θsin⁡2(−θ)\left(\frac{\tan^2\theta}{\sin^2\theta}-1\right)=\sec^2\theta\sin^2\left(-\theta\right)(sin2θtan2θ​−1)=sec2θsin2(−θ)﻿

Identify the most helpful first step in verifying the identity.
$\left(\frac{\tan^2\theta}{\sin^2\theta}-1\right)=\sec^2\theta\sin^2\left(-\theta\right)$