Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
0. Functions
Piecewise Functions
Problem 51b
Textbook Question
Area functions Let A(x) be the area of the region bounded by the t -axis and the graph of y=ƒ(t) from t=0 to t=x. Consider the following functions and graphs.
b. Find A(6).
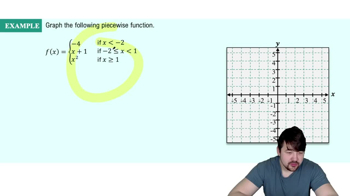
ƒ(t) = {-2t+8 if t ≤ 3 ; 2 if t >3 <IMAGE>
 Verified step by step guidance
Verified step by step guidance1
Identify the piecewise function \( f(t) = \begin{cases} -2t + 8, & \text{if } t \leq 3 \\ 2, & \text{if } t > 3 \end{cases} \).
To find \( A(6) \), calculate the area under the curve from \( t = 0 \) to \( t = 6 \).
For \( 0 \leq t \leq 3 \), integrate \( -2t + 8 \) with respect to \( t \).
For \( 3 < t \leq 6 \), integrate \( 2 \) with respect to \( t \).
Add the results of the two integrals to find the total area \( A(6) \).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Area Under a Curve
The area under a curve represents the integral of a function over a specified interval. In this context, the area function A(x) calculates the total area between the curve y = f(t) and the t-axis from t = 0 to t = x. This concept is fundamental in calculus as it connects geometric interpretations with integral calculus.
Recommended video:
Summary of Curve Sketching Example 2
Piecewise Functions
A piecewise function is defined by different expressions based on the input value. In the given problem, f(t) is defined differently for t ≤ 3 and t > 3, which requires careful consideration when calculating the area A(6). Understanding how to evaluate piecewise functions is crucial for accurately determining the area under the curve.
Recommended video:
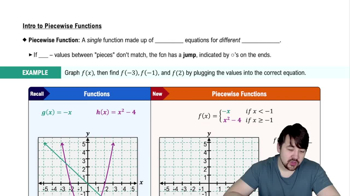
Piecewise Functions
Definite Integrals
Definite integrals are used to compute the area under a curve between two points. To find A(6), one must evaluate the integral of f(t) from 0 to 6, taking into account the different expressions of f(t) over the relevant intervals. This concept is essential for solving problems involving area functions and understanding the accumulation of quantities.
Recommended video:

Introduction to Indefinite Integrals
Related Videos
Related Practice