Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
0. Functions
Transformations
Problem 59
Textbook Question
Use shifts and scalings to graph the given functions. Then check your work with a graphing utility. Be sure to identify an original function on which the shifts and scalings are performed.
 Verified step by step guidance
Verified step by step guidance1
Identify the original function: The original function is f(x) = x^2, which is a basic parabola opening upwards.
Apply the vertical scaling: The function g(x) = -3x^2 involves a vertical scaling by a factor of 3. This means the parabola becomes narrower compared to f(x) = x^2.
Apply the reflection: The negative sign in front of the 3 indicates a reflection over the x-axis. This means the parabola, which originally opened upwards, now opens downwards.
Combine the transformations: The transformations applied to f(x) = x^2 result in the function g(x) = -3x^2, which is a downward-opening parabola that is narrower than the original.
Verify with a graphing utility: Use a graphing calculator or software to plot g(x) = -3x^2 and confirm that it matches the described transformations.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
9mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Function Transformations
Function transformations involve shifting and scaling the graph of a function. Shifts can be vertical or horizontal, moving the graph up, down, left, or right, while scalings affect the graph's width and height. Understanding how these transformations affect the original function is crucial for accurately graphing the modified function.
Recommended video:
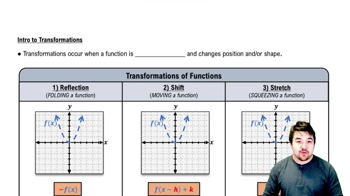
Intro to Transformations
Quadratic Functions
Quadratic functions are polynomial functions of degree two, typically expressed in the form f(x) = ax^2 + bx + c. The graph of a quadratic function is a parabola, which can open upwards or downwards depending on the sign of the coefficient 'a'. In this case, the function g(x) = -3x^2 represents a downward-opening parabola due to the negative coefficient.
Recommended video:

Introduction to Polynomial Functions
Graphing Utilities
Graphing utilities are software tools or calculators that allow users to visualize mathematical functions and their transformations. These tools can help verify the accuracy of hand-drawn graphs by providing a precise graphical representation. Utilizing a graphing utility is essential for confirming the results of shifts and scalings applied to the original function.
Recommended video:

Graphing The Derivative

 5:25m
5:25mWatch next
Master Intro to Transformations with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice

