Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
6. Derivatives of Inverse, Exponential, & Logarithmic Functions
Derivatives of Inverse Trigonometric Functions
Problem 3.10.80b
Textbook Question
Tracking a dive A biologist standing at the bottom of an 80-foot vertical cliff watches a peregrine falcon dive from the top of the cliff at a 45° angle from the horizontal (see figure). <IMAGE>
b. What is the rate of change of θ with respect to the bird’s height when it is 60 ft above the ground?
 Verified step by step guidance
Verified step by step guidance1
Identify the variables involved: Let θ be the angle of the falcon's dive with respect to the horizontal, and h be the height of the falcon above the ground.
Recognize the relationship between θ and h: Since the falcon is diving at a 45° angle, we can use trigonometric relationships. Specifically, tan(θ) = (80 - h) / x, where x is the horizontal distance from the base of the cliff to the falcon.
Differentiate the relationship with respect to time t: Use implicit differentiation on both sides of the equation tan(θ) = (80 - h) / x to find dθ/dt in terms of dh/dt and dx/dt.
Apply the chain rule: Differentiate tan(θ) with respect to t to get sec²(θ) * (dθ/dt) = (dx/dt * (80 - h) - x * dh/dt) / x².
Substitute known values: When the falcon is 60 ft above the ground, h = 60. Use the given angle and any additional information about the falcon's speed or horizontal distance to solve for dθ/dt.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
11mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Related Rates
Related rates involve finding the rate at which one quantity changes in relation to another. In this problem, we need to determine how the angle θ changes as the height of the falcon changes. This concept is essential for solving problems where multiple variables are interdependent and change over time.
Recommended video:
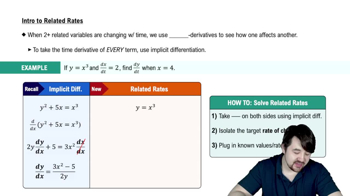
Intro To Related Rates
Trigonometric Functions
Trigonometric functions, such as sine, cosine, and tangent, relate the angles of a triangle to the lengths of its sides. In this scenario, the angle θ is related to the height of the falcon and the horizontal distance from the cliff. Understanding these functions is crucial for establishing the relationship between the angle and the height.
Recommended video:

Introduction to Trigonometric Functions
Differentiation
Differentiation is a fundamental concept in calculus that involves finding the derivative of a function, which represents the rate of change of that function. To find the rate of change of θ with respect to the bird's height, we will need to apply differentiation to the relationship established by the trigonometric functions, allowing us to compute how quickly the angle changes as the falcon descends.
Recommended video:

Finding Differentials

 7:26m
7:26mWatch next
Master Derivatives of Inverse Sine & Inverse Cosine with a bite sized video explanation from Callie
Start learning



