Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
4. Applications of Derivatives
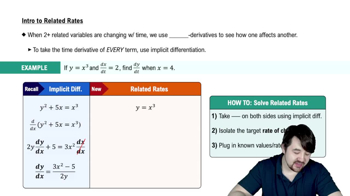
Related Rates
Problem 29c
Textbook Question
Consider the following cost functions.
c. Interpret the values obtained in part (b).
C(x) = 1000+0.1x, 0≤x≤5000, a=2000
 Verified step by step guidance
Verified step by step guidance1
Identify the cost function given: \( C(x) = 1000 + 0.1x \). This function represents the total cost in terms of the number of units \( x \).
Understand the domain of the function: \( 0 \leq x \leq 5000 \). This means the function is valid for any number of units between 0 and 5000.
In part (b), you likely calculated the cost at a specific value of \( x \), such as \( x = 2000 \). Substitute \( x = 2000 \) into the cost function to find \( C(2000) \).
Calculate \( C(2000) = 1000 + 0.1 \times 2000 \). This will give you the total cost when 2000 units are produced.
Interpret the result: The value obtained from \( C(2000) \) represents the total cost of producing 2000 units. The fixed cost is 1000, and the variable cost is 0.1 per unit, which contributes to the total cost based on the number of units produced.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Cost Function
A cost function represents the total cost incurred by a business in producing a certain quantity of goods, denoted as C(x). In this case, C(x) = 1000 + 0.1x indicates that there is a fixed cost of 1000 and a variable cost of 0.1 per unit produced. Understanding this function is crucial for analyzing how costs change with production levels.
Recommended video:

Properties of Functions
Interpretation of Values
Interpreting values from a cost function involves understanding what the numerical outputs signify in a real-world context. For instance, if x represents the number of units produced, the output of C(x) provides insights into total costs at different production levels, helping businesses make informed decisions about pricing and production.
Recommended video:

Average Value of a Function
Constraints on Production
The constraint 0 ≤ x ≤ 5000 indicates the permissible range of production levels for the cost function. This means that the analysis is limited to producing between 0 and 5000 units. Recognizing these constraints is essential for accurately interpreting the cost function and understanding its implications for business operations.
Recommended video:

The Product Rule
Related Videos
Related Practice