Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
Inverse Trigonometric Functions
Problem 80
Textbook Question
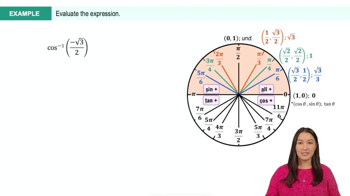
Evaluating inverse trigonometric functions Without using a calculator, evaluate the following expressions.
tan−1(tan(43π))
 Verified step by step guidance
Verified step by step guidance1
Understand the problem: We need to evaluate \( \tan^{-1}(\tan(\frac{3\pi}{4})) \). This involves understanding the behavior of the tangent function and its inverse.
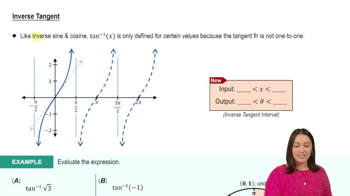
Recall the range of \( \tan^{-1}(x) \), which is \( (-\frac{\pi}{2}, \frac{\pi}{2}) \). The inverse tangent function will return an angle within this range.
Evaluate \( \tan(\frac{3\pi}{4}) \). The angle \( \frac{3\pi}{4} \) is in the second quadrant, where the tangent function is negative. Specifically, \( \tan(\frac{3\pi}{4}) = -1 \).
Now, find \( \tan^{-1}(-1) \). Since \( \tan^{-1}(x) \) returns an angle in \( (-\frac{\pi}{2}, \frac{\pi}{2}) \), we need to find an angle in this range whose tangent is \(-1\).
The angle that satisfies \( \tan(\theta) = -1 \) within the range \( (-\frac{\pi}{2}, \frac{\pi}{2}) \) is \( -\frac{\pi}{4} \). Therefore, \( \tan^{-1}(\tan(\frac{3\pi}{4})) = -\frac{\pi}{4} \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Related Videos
Related Practice