Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
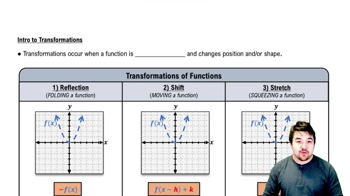
Transformations
Problem 1.2.10
Textbook Question
How do you obtain the graph of y=−3f(x) from the graph of y=f(x)?
 Verified step by step guidance
Verified step by step guidance1
Start with the graph of y = f(x). This is your original function graph.
The transformation y = -3f(x) involves two operations: a vertical reflection and a vertical stretch.
First, apply a vertical reflection across the x-axis. This changes the graph of y = f(x) to y = -f(x), flipping it upside down.
Next, apply a vertical stretch by a factor of 3. This means you multiply all y-values of the graph by 3, making the graph taller by stretching it away from the x-axis.
Combine these transformations to obtain the final graph of y = -3f(x), which is the vertically stretched and reflected version of the original graph y = f(x).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?

 5:25m
5:25mWatch next
Master Intro to Transformations with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice