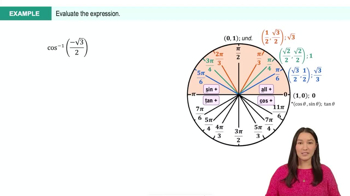
Evaluating inverse trigonometric functions Without using a calculator, evaluate the following expressions.
$\tan\left(\tan^{-1}1\right)$

Verified step by step guidance

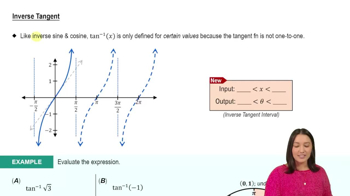
1. Understand the problem: We need to evaluate \( \tan(\tan^{-1}(1)) \). This involves the inverse trigonometric function \( \tan^{-1} \), which is the inverse of the tangent function.
2. Recall the definition of \( \tan^{-1}(x) \): It is the angle \( \theta \) such that \( \tan(\theta) = x \) and \( \theta \) is in the range \(-\frac{\pi}{2} < \theta < \frac{\pi}{2} \).
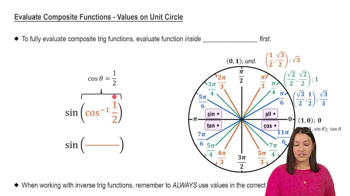
3. Apply the definition to \( \tan^{-1}(1) \): We need to find an angle \( \theta \) such that \( \tan(\theta) = 1 \). The angle \( \theta \) that satisfies this within the range is \( \frac{\pi}{4} \), because \( \tan(\frac{\pi}{4}) = 1 \).
4. Substitute back into the original expression: Now that we know \( \tan^{-1}(1) = \frac{\pi}{4} \), we substitute this into the expression to get \( \tan(\frac{\pi}{4}) \).
5. Evaluate \( \tan(\frac{\pi}{4}) \): Since \( \tan(\frac{\pi}{4}) = 1 \), the expression \( \tan(\tan^{-1}(1)) \) simplifies to 1.