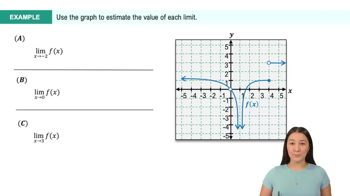
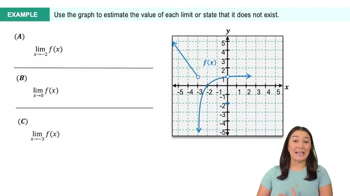
a. Use a graphing utility to estimate lim x→0 tan 2x / sin x, lim x→0 tan 3x / sin x, and lim x→0 tan 4x / sin x.

Verified step by step guidance

1. To estimate the limits using a graphing utility, first understand the expressions: lim x→0 tan(2x) / sin(x), lim x→0 tan(3x) / sin(x), and lim x→0 tan(4x) / sin(x). These involve trigonometric functions where x approaches 0.
2. Graph each function separately: y = tan(2x) / sin(x), y = tan(3x) / sin(x), and y = tan(4x) / sin(x). Use a graphing calculator or software to plot these functions over an interval around x = 0, such as [-0.1, 0.1].
3. Observe the behavior of each graph as x approaches 0. The limit is the value that the function approaches as x gets closer to 0. Look for a horizontal line or a point where the function stabilizes near x = 0.
4. For each function, note the y-value that the graph approaches as x approaches 0. This y-value is the estimated limit for each expression.
5. Compare the estimated limits for each function. Notice any patterns or differences in the limits as the coefficient of x in the tangent function changes from 2 to 3 to 4.

Key Concepts

Limits

A limit is a fundamental concept in calculus that describes the behavior of a function as its input approaches a certain value. In this case, we are interested in the limits of the functions tan(kx) and sin(x) as x approaches 0. Understanding limits is crucial for evaluating expressions that may be indeterminate at specific points.

Trigonometric Functions

Trigonometric functions, such as sine and tangent, are periodic functions that relate angles to ratios of sides in right triangles. The behavior of these functions near specific points, like x = 0, is essential for evaluating limits. For small angles, both tan(x) and sin(x) can be approximated, which simplifies the limit calculations.

L'Hôpital's Rule

L'Hôpital's Rule is a method used to evaluate limits of indeterminate forms, such as 0/0 or ∞/∞. It states that if the limit of f(x)/g(x) results in an indeterminate form, the limit can be found by taking the derivative of the numerator and the derivative of the denominator. This rule can be particularly useful when dealing with limits involving trigonometric functions.