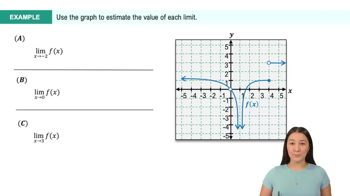
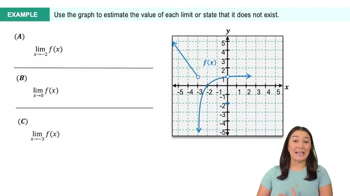
Suppose x lies in the interval (1, 3) with x≠2. Find the smallest positive value of δ such that the inequality 0<|x−2|<δ is true.

Verified step by step guidance

1. Identify the point of interest, which is x = 2, and note that we want to find δ such that x is within the interval (1, 3) but not equal to 2.
2. Rewrite the inequality |x - 2| < δ to express it in terms of x: this means we want the distance between x and 2 to be less than δ.
3. Determine the bounds for x based on the interval (1, 3) while ensuring x ≠ 2. This means we need to consider the distances from 2 to the endpoints of the interval.
4. Calculate the distances from 2 to the nearest endpoints of the interval: the distance from 2 to 1 is |2 - 1| = 1, and the distance from 2 to 3 is |2 - 3| = 1.
5. Since δ must be less than both distances, the smallest positive value of δ that satisfies the inequality is the minimum of these distances, which is 1.