Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
0. Functions
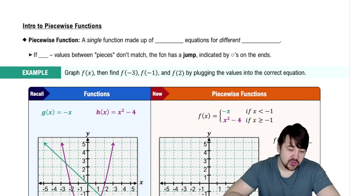
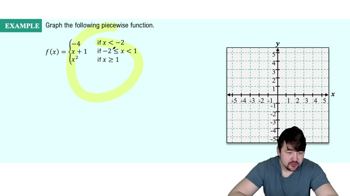
Piecewise Functions
Problem 76
Textbook Question
Roots and powers Sketch a graph of the given pairs of functions. Be sure to draw the graphs accurately relative to each other.
y = (x)¹⸍³ and y = (x)¹⸍⁵
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the functions y = x^{1/3} and y = x^{1/5}. These are both root functions, where y = x^{1/3} is the cube root of x and y = x^{1/5} is the fifth root of x.
Step 2: Analyze the domain and range of both functions. Both functions are defined for all real numbers x, meaning their domain is (-∞, ∞). The range for both functions is also (-∞, ∞) because any real number can be a cube root or fifth root.
Step 3: Consider the behavior of the functions as x approaches positive and negative infinity. As x approaches positive infinity, both y = x^{1/3} and y = x^{1/5} will increase, but y = x^{1/3} will increase faster than y = x^{1/5}. As x approaches negative infinity, both functions will decrease, but again, y = x^{1/3} will decrease faster than y = x^{1/5}.
Step 4: Identify key points to plot. For both functions, when x = 0, y = 0. For x = 1, y = 1 for both functions. For x = -1, y = -1 for both functions. These points will help in sketching the graphs accurately.
Step 5: Sketch the graphs. Start by plotting the key points identified in Step 4. Then, draw smooth curves through these points, ensuring that the graph of y = x^{1/3} is steeper than y = x^{1/5} for both positive and negative values of x.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Roots and Powers
Roots and powers are fundamental concepts in algebra and calculus that describe the relationship between numbers and their exponents. A power, such as x raised to a fraction, indicates how many times to multiply x by itself, while a root, like the cube root or fifth root, represents the value that, when raised to a specific power, yields the original number. Understanding these concepts is crucial for analyzing the behavior of functions defined by such expressions.
Recommended video:

The Power Rule
Graphing Functions
Graphing functions involves plotting points on a coordinate system to visually represent the relationship between the input (x-values) and output (y-values) of a function. For the functions y = x^(1/3) and y = x^(1/5), it is important to understand their shapes, intercepts, and asymptotic behavior. Accurate graphing allows for a comparative analysis of how these functions behave relative to each other, particularly in terms of growth rates and curvature.
Recommended video:

Graph of Sine and Cosine Function
Behavior of Radical Functions
Radical functions, such as y = x^(1/3) and y = x^(1/5), exhibit unique characteristics based on their roots. The cube root function is defined for all real numbers and has a point of inflection at the origin, while the fifth root function also spans all real numbers but grows more slowly than the cube root as x increases. Understanding these behaviors is essential for accurately sketching their graphs and comparing their growth and shape.
Recommended video:

Limits of Rational Functions with Radicals
Related Videos
Related Practice