Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
5. Graphical Applications of Derivatives
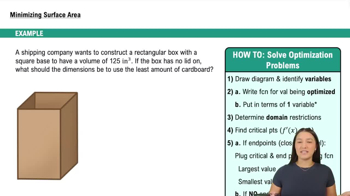
Applied Optimization
Problem 74b
Textbook Question
The arbelos An arbelos is the region enclosed by three mutually tangent semicircles; it is the region inside the larger semicircle and outside the two smaller semicircles (see figure). <IMAGE>
b. Show that the area of the arbelos is the area of a circle whose diameter is the distance BD in the figure.
 Verified step by step guidance
Verified step by step guidance1
Identify the semicircles: Consider the larger semicircle with diameter AC and two smaller semicircles with diameters AB and BC, where B is the point of tangency between the two smaller semicircles.
Calculate the area of the larger semicircle: The area of a semicircle is given by \( \frac{1}{2} \pi r^2 \), where \( r \) is the radius. For the larger semicircle, the radius is \( \frac{AC}{2} \).
Calculate the area of the two smaller semicircles: Similarly, calculate the areas of the semicircles with diameters AB and BC. The radii are \( \frac{AB}{2} \) and \( \frac{BC}{2} \) respectively.
Determine the area of the arbelos: Subtract the sum of the areas of the two smaller semicircles from the area of the larger semicircle to find the area of the arbelos.
Relate the area of the arbelos to a circle: Show that this area is equivalent to the area of a circle with diameter BD. Use the formula for the area of a circle \( \pi \left( \frac{d}{2} \right)^2 \), where \( d \) is the diameter, and verify that it matches the area of the arbelos.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
8mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Arbelos Definition
An arbelos is a geometric figure formed by three mutually tangent semicircles. It consists of one larger semicircle that encompasses two smaller semicircles, all sharing a common tangent point. Understanding the configuration of these semicircles is crucial for analyzing the area and properties of the arbelos.
Recommended video:

Definition of the Definite Integral
Area of Semicircles
The area of a semicircle can be calculated using the formula A = (1/2)πr², where r is the radius. In the context of the arbelos, the areas of the individual semicircles contribute to the overall area of the arbelos. Recognizing how to compute these areas is essential for deriving the area of the arbelos.
Recommended video:

Estimating the Area Under a Curve with Right Endpoints & Midpoint
Circle Area Relation
The area of a circle is given by the formula A = π(d/2)², where d is the diameter. In the problem, it is stated that the area of the arbelos can be expressed as the area of a circle with a diameter equal to the distance BD. Understanding this relationship allows for the comparison and calculation of areas between the arbelos and the circle.
Recommended video:
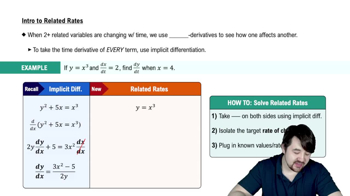
Intro To Related Rates

 1:13m
1:13mWatch next
Master Intro to Applied Optimization: Maximizing Area with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice