Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
2. Intro to Derivatives
Tangent Lines and Derivatives
Problem 18a
Textbook Question
Use definition (1) (p. 133) to find the slope of the line tangent to the graph of f at P.
f(x) = 4/x2; P(-1,4)
 Verified step by step guidance
Verified step by step guidance1
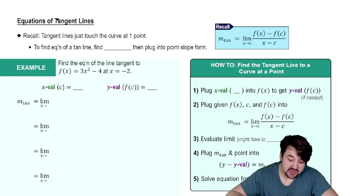
Step 1: Recall the definition of the derivative as the slope of the tangent line at a point. The derivative of a function f at a point x is given by the limit: f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}.
Step 2: Identify the function f(x) = \frac{4}{x^2} and the point P(-1, 4). We need to find the derivative of f at x = -1.
Step 3: Substitute f(x) = \frac{4}{x^2} into the derivative definition: f'(x) = \lim_{h \to 0} \frac{\frac{4}{(x+h)^2} - \frac{4}{x^2}}{h}.
Step 4: Simplify the expression inside the limit. Find a common denominator for the fractions: \frac{4}{(x+h)^2} - \frac{4}{x^2} = \frac{4x^2 - 4(x+h)^2}{x^2(x+h)^2}.
Step 5: Simplify further and evaluate the limit as h approaches 0 to find f'(-1), which gives the slope of the tangent line at P(-1, 4).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Tangent Line
A tangent line to a curve at a given point is a straight line that touches the curve at that point without crossing it. The slope of the tangent line represents the instantaneous rate of change of the function at that point, which is crucial for understanding how the function behaves locally.
Recommended video:
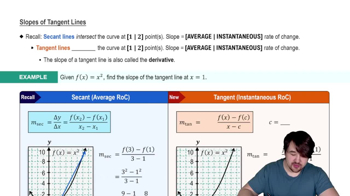
Slopes of Tangent Lines
Derivative
The derivative of a function at a point quantifies how the function's output changes as its input changes. It is defined as the limit of the average rate of change of the function as the interval approaches zero. In this context, finding the derivative of f(x) = 4/x² will provide the slope of the tangent line at point P.
Recommended video:

Derivatives
Limit Definition of Derivative
The limit definition of the derivative states that the derivative f'(a) at a point a is the limit of the difference quotient as h approaches zero: f'(a) = lim (h→0) [(f(a+h) - f(a))/h]. This definition is fundamental for calculating the slope of the tangent line, as it formalizes the concept of instantaneous rate of change.
Recommended video:

Definition of the Definite Integral

 5:13m
5:13mWatch next
Master Slopes of Tangent Lines with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice