Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
1. Limits and Continuity
Continuity
Problem 2.7b
Textbook Question
Limits and Continuity
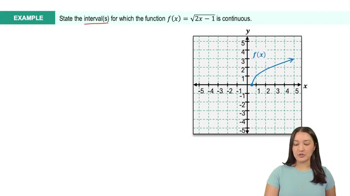
On what intervals are the following functions continuous?
b. g(x) = x³/⁴
 Verified step by step guidance
Verified step by step guidance1
Identify the type of function: The function g(x) = x^(3/4) is a power function, which is generally continuous wherever it is defined.
Determine the domain of the function: Since the exponent 3/4 is a positive rational number, g(x) is defined for all x ≥ 0. This is because the fourth root of a negative number is not real.
Check for any points of discontinuity: For power functions like g(x) = x^(3/4), there are no discontinuities within their domain. Therefore, the function is continuous on its entire domain.
Conclude the intervals of continuity: Since g(x) is defined and continuous for all x ≥ 0, the interval of continuity is [0, ∞).
Summarize the findings: The function g(x) = x^(3/4) is continuous on the interval [0, ∞), as it is a power function with a domain of all non-negative real numbers.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Limits
Limits are fundamental in calculus, representing the value that a function approaches as the input approaches a certain point. Understanding limits is crucial for analyzing the behavior of functions, especially at points where they may not be explicitly defined. They help determine continuity and differentiability, which are essential for evaluating functions over intervals.
Recommended video:

One-Sided Limits
Continuity
A function is continuous at a point if the limit of the function as it approaches that point equals the function's value at that point. For a function to be continuous over an interval, it must be continuous at every point within that interval. This concept is vital for understanding how functions behave and ensuring that there are no breaks, jumps, or holes in their graphs.
Recommended video:

Intro to Continuity
Piecewise Functions
Piecewise functions are defined by different expressions over different intervals. Analyzing these functions requires checking continuity at the boundaries of the pieces to ensure that the function behaves consistently. Understanding how to evaluate these functions across their defined intervals is essential for determining where they are continuous.
Recommended video:
Piecewise Functions
Related Videos
Related Practice