Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
4. Applications of Derivatives
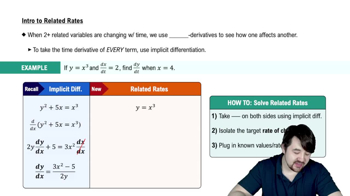
Related Rates
Problem 3.11.30
Textbook Question
Parabolic motion An arrow is shot into the air and moves along the parabolic path y=x(50−x) (see figure). The horizontal component of velocity is always 30 ft/s. What is the vertical component of velocity when (a) x=10 and (b) x=40? <IMAGE>
 Verified step by step guidance
Verified step by step guidance1
First, understand that the path of the arrow is given by the equation y = x(50 - x). This is a parabolic equation representing the vertical position y as a function of the horizontal position x.
To find the vertical component of velocity, we need to determine the derivative of y with respect to time t, which is dy/dt. However, y is given as a function of x, so we will use the chain rule: dy/dt = (dy/dx) * (dx/dt).
The horizontal component of velocity is given as dx/dt = 30 ft/s. This is constant throughout the motion.
Next, find dy/dx by differentiating y = x(50 - x) with respect to x. This gives dy/dx = 50 - 2x.
Now, substitute dy/dx and dx/dt into the chain rule expression: dy/dt = (50 - 2x) * 30. This expression gives the vertical component of velocity as a function of x. Evaluate this expression for (a) x = 10 and (b) x = 40 to find the vertical component of velocity at these points.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Parabolic Motion
Parabolic motion refers to the trajectory of an object that is influenced by gravity, resulting in a curved path. In this case, the motion of the arrow follows a parabolic equation, which describes how the vertical position (y) changes with respect to the horizontal position (x). Understanding this concept is crucial for analyzing the motion of projectiles and determining their velocity components.
Recommended video:

Derivatives Applied To Velocity
Velocity Components
Velocity is a vector quantity that has both magnitude and direction. In projectile motion, the total velocity can be broken down into horizontal and vertical components. The horizontal component remains constant (30 ft/s in this case), while the vertical component changes due to gravitational acceleration. Calculating these components at specific points along the trajectory is essential for understanding the arrow's motion.
Recommended video:

Derivatives Applied To Velocity
Differentiation
Differentiation is a fundamental concept in calculus that involves finding the rate at which a function changes at any given point. In the context of this problem, differentiating the parabolic equation y = x(50 - x) with respect to x allows us to determine the vertical component of velocity, which is the derivative of the height with respect to time. This mathematical tool is vital for analyzing motion and finding instantaneous rates.
Recommended video:

Finding Differentials
Related Videos
Related Practice