Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
4. Applications of Derivatives
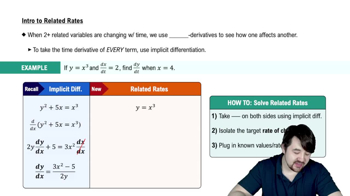
Related Rates
Problem 3.6.5
Textbook Question
Suppose w(t) is the weight (in pounds) of a golden retriever puppy t weeks after it is born. Interpret the meaning of w'(15) = 1.75.
 Verified step by step guidance
Verified step by step guidance1
Understand that w(t) represents the weight of the puppy as a function of time, where t is measured in weeks.
Recognize that w'(t) is the derivative of w(t) with respect to t, which represents the rate of change of the puppy's weight with respect to time.
The expression w'(15) = 1.75 indicates that at t = 15 weeks, the rate of change of the puppy's weight is 1.75 pounds per week.
Interpret this to mean that when the puppy is 15 weeks old, its weight is increasing at a rate of 1.75 pounds each week.
This rate of change is an instantaneous rate, meaning it describes how fast the weight is increasing exactly at 15 weeks, not over an interval of time.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Derivative Interpretation
The derivative of a function at a given point represents the rate of change of that function at that point. In this context, w'(15) indicates how the weight of the puppy is changing at 15 weeks. Specifically, it tells us that the weight is increasing at a rate of 1.75 pounds per week at that time.
Recommended video:

Derivatives
Function Notation
Function notation, such as w(t), is used to express the relationship between an independent variable (t, in this case, time in weeks) and a dependent variable (w, the weight of the puppy). Understanding this notation is crucial for interpreting the behavior of the function over time and how changes in t affect w.
Recommended video:

Sigma Notation
Contextual Interpretation
Interpreting the meaning of mathematical results in context is essential. Here, w'(15) = 1.75 means that at 15 weeks, the puppy's weight is not just increasing, but it is doing so at a specific rate, which can inform decisions about its health and growth patterns. This contextual understanding helps relate mathematical concepts to real-world scenarios.
Recommended video:

The Power Rule: Negative & Rational Exponents Example 3
Related Videos
Related Practice