Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
3. Techniques of Differentiation
Product and Quotient Rules
Problem 62a
Textbook Question
Find an equation of the line tangent to the given curve at a.
y = 2x2 / (3x - 1); a = 1
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the function and the point of tangency. The function given is \( y = \frac{2x^2}{3x - 1} \) and the point of tangency is at \( a = 1 \).
Step 2: Find the derivative of the function to determine the slope of the tangent line. Use the quotient rule: if \( y = \frac{u}{v} \), then \( y' = \frac{u'v - uv'}{v^2} \). Here, \( u = 2x^2 \) and \( v = 3x - 1 \).
Step 3: Calculate \( u' \) and \( v' \). For \( u = 2x^2 \), \( u' = 4x \). For \( v = 3x - 1 \), \( v' = 3 \).
Step 4: Substitute \( u, u', v, \) and \( v' \) into the quotient rule formula to find \( y' \). Simplify the expression to get the derivative.
Step 5: Evaluate the derivative at \( x = 1 \) to find the slope of the tangent line at the point \( a = 1 \). Use the point-slope form of a line, \( y - y_1 = m(x - x_1) \), where \( m \) is the slope and \( (x_1, y_1) \) is the point on the curve.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Tangent Line
A tangent line to a curve at a given point is a straight line that touches the curve at that point without crossing it. The slope of the tangent line represents the instantaneous rate of change of the function at that point, which can be found using the derivative.
Recommended video:
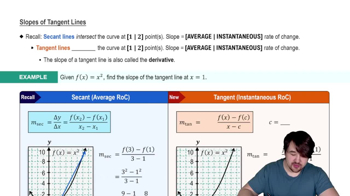
Slopes of Tangent Lines
Derivative
The derivative of a function measures how the function's output value changes as its input value changes. It is calculated as the limit of the average rate of change of the function over an interval as the interval approaches zero. For a function y = f(x), the derivative f'(x) gives the slope of the tangent line at any point x.
Recommended video:

Derivatives
Point-Slope Form
The point-slope form of a linear equation is used to write the equation of a line when the slope and a point on the line are known. It is expressed as y - y₁ = m(x - x₁), where m is the slope and (x₁, y₁) is the point. This form is particularly useful for finding the equation of the tangent line once the slope has been determined.
Recommended video:
Guided course
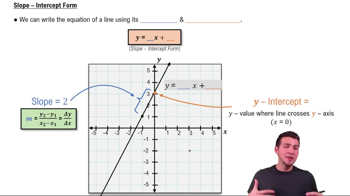
Slope-Intercept Form
Related Videos
Related Practice










