Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
4. Applications of Derivatives
Related Rates
Problem 6a
Textbook Question
At all times, the length of a rectangle is twice the width w of the rectangleas the area of the rectangle changes with respect to time t.
a. Find an equation relating A to w.
 Verified step by step guidance
Verified step by step guidance1
Start by recalling the formula for the area of a rectangle, which is the product of its length and width: A = length × width.
According to the problem, the length of the rectangle is twice the width. Therefore, express the length in terms of the width: length = 2w.
Substitute the expression for the length into the area formula. This gives you A = 2w × w.
Simplify the equation to find the relationship between the area A and the width w: A = 2w^2.
This equation, A = 2w^2, now relates the area of the rectangle to its width, considering the given condition that the length is twice the width.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Area of a Rectangle
The area A of a rectangle is calculated using the formula A = length × width. In this case, since the length is twice the width (l = 2w), the area can be expressed as A = 2w × w = 2w². Understanding this relationship is crucial for deriving the equation that relates area to width.
Recommended video:

Estimating the Area Under a Curve Using Left Endpoints
Relationship Between Variables
In calculus, understanding how different variables relate to each other is essential. Here, the area A is a function of the width w, which means any change in w will affect A. This relationship is foundational for analyzing how the area changes as the width varies.
Recommended video:
Guided course
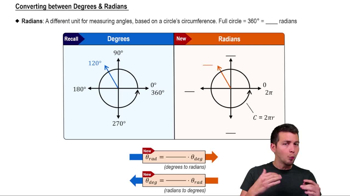
Converting between Degrees & Radians
Differentiation
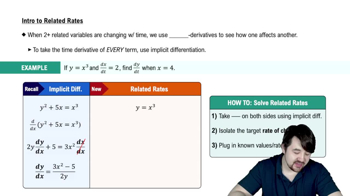
Differentiation is a key concept in calculus that deals with the rate of change of a function. If the problem requires finding how the area changes with respect to time, we would differentiate the area function A(w) with respect to w and then apply the chain rule to relate it to time t, allowing us to analyze the dynamics of the rectangle's area.
Recommended video:

Finding Differentials
Related Videos
Related Practice